Bilan énergétique, rendement
L’objectif est de déterminer comment l’énergie d’un système varie.
I. Schéma général
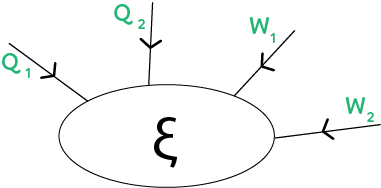
Il y a un rond avec la lettre Σ qui représente le système. On voit qu’il y a des interactions vis-à-vis de l’extérieur. Par convention, on remarque que toutes les flèches vont vers le système. On a noté 2 lettres : les « Q » et les « W ». Les « Q » correspondent à la quantité de chaleur (transferts thermiques) alors que les « W » sont pour des travaux mécaniques, électriques. Le système peut :
– Soit recevoir de l’énergie : sous forme d’une quantité de chaleur (Q > 0) dans le sens de la flèche, sous forme de travail mécanique ou électrique (W > 0) dans le sens de la flèche.
– Soit perdre ou délivrer de l’énergie : Q < 0, W < 0. L’énergie va dans le sens opposé à la flèche sur le schéma donc elle est négative et il y a perte/livraison d’énergie. De même pour le travail.
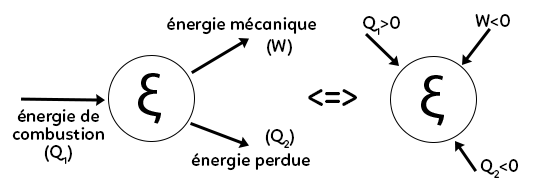
Par exemple, un moteur. On rajoute une petite subtilité car parfois on a des schémas avec des flèches qui ne sont pas toutes rentrantes. On a le système qui correspond au moteur. L’énergie de combustion arrive dans le système c’est pourquoi on met le plein d’essence dans la voiture. C’est cette énergie-là qui est fournie au moteur. Qu’en fait le moteur ?
Il crée de l’énergie mécanique qui permet de faire tourner les roues et il y a également une perte d’énergie. Est-ce que ce sont des travaux mécaniques ou des quantités de chaleur ?
L’énergie de combustion c’est une quantité de chaleur due à une réaction chimique. L’énergie mécanique c’est un travail mécanique (W). L’énergie perdue pourrait être discutée. Ici on décide de mettre la lettre Q. On dit, pour résumer, que l’énergie perdue est perdue sous forme de chaleur. Même si ce sont des frottements, c’est mécanique, mais les frottements induisent une perte thermique. Étant donné les flèches du schéma, Q1 est bien une quantité d’énergie qui rentre et donc Q1 est positif. L’énergie mécanique W sort et donc elle devrait être négative, mais non !
En fait, on a mis la flèche vers l’extérieur donc c’est déjà dans le bon sens et donc W > 0. Q2 est représenté avec une flèche vers l’extérieur donc Q2 est positif.
On peut aussi faire une représentation plus conventionnelle avec un système au milieu et des énergies qui rentrent. Q1 est l’énergie de combustion, elle rentre donc elle est positive. W est l’énergie mécanique, elle sort, or la flèche est rentrante donc on note W < 0. De même pour Q2.
II. Le rendement
C’est une quantité extrêmement utile. Si on achète une voiture, on préfère un rendement à 50 % du moteur plutôt qu’un rendement à 10 %. Idem pour un réfrigérateur par exemple. Plus le rendement s’approche de 100 %, meilleur est l’objet. Pourquoi ?
La définition du rendement est : $rendement = r = \dfrac{énergie \ utile}{énergie \ consommée}=\dfrac{puissance \ utile}{puissance \ consommée}$(en divisant en haut et en bas par $Δt.$)
C’est-à-dire que si on arrive à un rendement de 100 %, on a autant d’énergie utile que d’énergie consommée. Ce serait l’idéal mais en réalité, c’est quasiment impossible. Voici deux exemples :
A. Le moteur
Quelle est l’énergie utile dans le moteur ? C’est le travail fourni, l’énergie mécanique, l’énergie fournie aux roues pour qu’elles tournent. On l’a appelé précédemment W. Positif ou négatif en fonction de la convention adoptée sur le schéma. L’énergie consommée c’est l’énergie électrique pour une voiture électrique ou thermique pour les autres voitures (essence, GPL…). $r = \dfrac{W}{Q1}$ le tout en valeur absolue.
On met la valeur absolue pour éviter de devoir discuter de la convention adoptée. Que W soit négatif ou positif, il devient positif avec la valeur absolue. De même pour Q1.
B. Le réfrigérateur
Le réfrigérateur sert à refroidir les aliments. L’énergie utile c’est la chaleur prélevée aux aliments. L’énergie consommée c’est l’énergie électrique car on branche le réfrigérateur à une prise électrique. C’est l’énergie électrique qui va être prélevée par la prise électrique. On a donc la formule du rendement : $r = \dfrac{chaleur \ prélevée}{énergie \ électrique \ consommée}$.
Bilan énergétique, variation de l'énergie interne
I. Source de variation : le travail
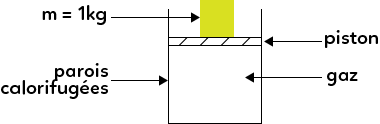
On prend l’exemple courant de la compression d’un piston. Les parois rectangulaires extérieures représentent le cylindre. Il est fermé par le piston, représenté en hachuré. Par-dessus, on a déposé une masse de 1 kg et à l’intérieur un gaz est emprisonné, il constitue notre système. Que se passe-t-il ?
Admettons que la masse d’un kilo ne soit pas présente, cela voudrait dire que le gaz à l’intérieur est dans le même état que celui à l’extérieur (pression, température). Que va-t-il se passer lorsqu’on appuie en mettant une masse de 1 kg dessus ?
Le gaz est comprimé, on le compresse. Par exemple, on fait l’expérience de prendre une pompe pour gonfler les pneus du vélo, si on bouche l’extrémité de la pompe c’est exactement comme si l’on mettait un piston. Maintenant si on appuie sur la pompe, c’est exactement comme si l’on mettait une masse. Sur le pouce à l’endroit où l’on bouche le trou, l’air est un peu plus chaud. Le système a tendance à chauffer lors de la compression.
Les équations nous rendent-elles compte de cet effet-là ?
Précisons que l’on suppose que les parois sont calorifugées. C’est-à-dire que de l’énergie, sous forme de chaleur, ne peut pas partir à travers les parois. Au niveau de la mise en équation, on commence par écrire ce qu’est le système ici. C’est le gaz qui est emprisonné.
On a alors : $ΔU = W + Q.$
Mais ici, comme les parois sont calorifugées on ne peut pas avoir d’échange de chaleur entre l’extérieur et le système. Il n’y a pas d’énergie apportée sous forme de chaleur.
Au final, on a $ΔU = W.$
Est-ce qu’on peut en déduire que la température va augmenter ? Oui, car on a vu dans d’autres cours sur les gaz que cette énergie interne elle est reliée à l’énergie cinétique macroscopique, celle-ci est liée à l’agitation des molécules qui composent le gaz. Cela signifie que si $ΔU > 0,$ l’énergie interne augmente et donc que l’énergie microscopique augmente. L’agitation des molécules augmentent et donc ça veut dire que la température de ce gaz est en train d’augmenter. Donc apporter un travail, avoir $W > 0$ induit que $ΔU > 0,$ et comme on vient de le dire, que la température augmente.
II. Source de variation : la quantité de chaleur
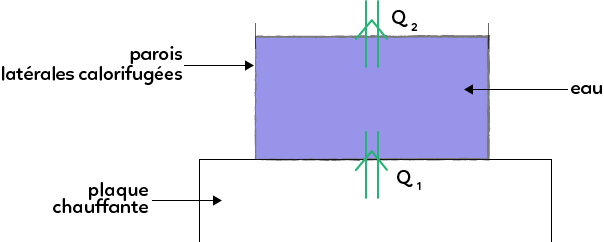
On prend un récipient avec de l’eau que l’on pose sur une plaque chauffante. On fait l’hypothèse que les parois latérales sont calorifugées.
L’énergie sous forme de chaleur ne peut pas partir sur les côtés. Par contre, l’énergie peut passer de la plaque chauffante à l’eau et on va dire que la chaleur, l’énergie qui passe s’appelle Q1. On suppose aussi que de l’énergie ressort au niveau de l’interface eau/air, on la note Q2. Le système c’est l’eau.
On a alors : $ΔU =W+Q_1 – Q_2$
Ici, il n’y a pas de travail mécanique, on ne vient pas compresser le liquide. Or pour un état condensé, on a aussi vu dans un autre cours qui concerne l’énergie interne et les états condensés, que $ΔU$ peut aussi s’exprimer comme cela :
$ ΔU =m_{eau} \times c_{eau} \times ΔT$.
On parle d’eau ici car le système c’est de l’eau. En égalisant ces deux équations portant sur l’énergie interne on peut isoler $ΔT$ et écrire que :
$ ΔT = \dfrac{Q_1-Q_2}{m_{eau} \times c_{eau}}$.
On suppose qu’on a mis un couvercle ce qui fait que l’on peut négliger la valeur de Q2 vis-à-vis de Q1.
Elle n’apparaît donc plus ici : $ΔT = \dfrac{Q_1}{m_{eau} \times c_{eau}}$.
N’oublions pas que Q1 est une énergie donc une puissance donc $Q_1 = P_1\times Δt$.
On a alors : $ΔT = \dfrac{P_1\times Δt }{m_{eau} \times c_{eau}}$.
$Δt$ étant le temps de chauffage.
Pour l’application numérique, on prend une plaque chauffante de 1000 W qui chauffe pendant 60 s. On prend une masse d’eau de 1 kg et la capacité thermique massique de l’eau vaut 4185 SI. En faisant l’application numérique, on trouve que $ΔT$ vaut environ 14°C. Au-delà de la valeur numérique, il faut remarquer que $ΔT$ est proportionnel à $Δt$ le temps de chauffage. C’est-à-dire que si on fait chauffer deux fois plus longtemps cette masse d’eau, on aura une élévation de température deux fois plus grande. Il y a une proportionnalité entre le temps de chauffage et la variation de température du système.