La poussée d'Archimède
La poussée d’Archimède
I. Origine de cette poussée
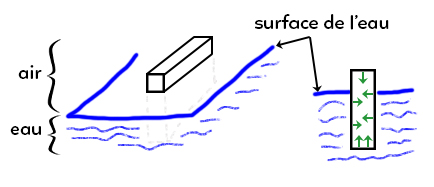
La poussée d’Archimède est, par exemple, la poussée qui permet à un bateau de flotter. Sur le premier schéma, nous pouvons voir un plan qui sépare l’air de l’eau ainsi qu’un objet qui est à la fois dans l’air et dans l’eau (vue en 3D). Sur le deuxième schéma, nous observons la même chose mais avec une vue en coupe. On retrouve donc la surface de l’eau avec une partie de l’objet qui est dans l’air et une autre qui est dans l’eau : il flotte. Pourquoi y a-t-il une force verticale qui permet à l’objet de ne pas couler ?
Ce sont les forces de pression qui en sont responsables. Ces forces de pression s’exercent partout où il y a un fluide à côté d’une paroi, et le fluide exerce donc une pression perpendiculaire à la paroi. Nous le voyons sur le schéma avec les flèches qui vont de l’extrémité droite vers la gauche et inversement, de telle sorte que ces forces se compensent. En revanche, sur la partie basse de l’objet, il s’exerce des forces perpendiculaires qui vont vers le haut. On retrouve aussi en haut des forces qui vont vers le bas, cependant ces forces sont plus petites que celles exercées sur le bas de l’objet. Cela engendre une force « globale » vers le haut.
Ce sont alors ces superpositions de forces de pression qui constitue ce que l’on appelle la poussée d’Archimède.
II. L’expression de la poussée d’Archimède
Cette force (la poussée d’Archimède) est l’opposée du poids du fluide déplacé. Il existe deux grandes distinctions :
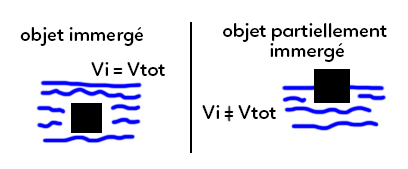
– le cas d’un objet complètement immergé dans un fluide,
– le cas d’un objet partiellement immergé dans un fluide.
La différence fondamentale se trouve dans le volume immergé.
Dans le premier cas où il est immergé totalement, le volume immergé est donc le volume de l’objet, le volume total.
Dans le deuxième cas où il est immergé partiellement, le volume immergé n’est pas tout à fait le volume total car il y a une partie du volume qui reste au-dessus de la surface.
On a donc $\overrightarrow{\Pi}$ la poussée d’Archimède. Cette poussée est une force et s’exprime donc en newton.
Soit $ \overrightarrow{\Pi} = -m_{fluide \ déplacé} \times \overrightarrow{g}$ car on sait que $p = m \times g.$
Qu’est-ce que c’est que la masse du fluide déplacé ?
On sait que pour un fluide, sa masse est égale à sa masse volumique multipliée par le volume.
Donc $ \overrightarrow{\Pi} = -\rho_{fluide} \times V_{immergé} \times \overrightarrow{g}$
On ne prend en compte que le volume immergé car il n’y a que cette partie qui a déplacé du fluide. En effet, le liquide a été déplacé puisque l’on a inséré un objet à la place.
III. Les applications
Il existe de nombreuses applications (comme les icebergs, les montgolfières, etc.). Ici nous allons voir quelle est la proportion immergée d’un iceberg.
Données :
$\rho_{glace} = \rho_g = 917 \ kg/m^3$
$ \rho_{liquide} = \rho_l = 1025 \ kg/m^3$
L’iceberg est statique. Cela veut dire que la somme des forces qui s’appliquent sur lui vaut zéro. Puisqu’il n’y en a que deux (son poids et la poussée d’Archimède), alors :
$\| \overrightarrow{P} \| = \| \overrightarrow{\Pi} \|$
D’où : $ m_{tot} \times g = m_{fluide \ déplacé} \times g$
Donc, $\rho_g \times V_{tot} = \rho_l \times V_{immergé},$ ici les $g$ se sont simplifiés.
Alors, $\dfrac{ V_{immergé} }{ V_{tot} } = \dfrac{ \rho_g }{ \rho_l } \backsimeq 89,5 \%$
Avec $\dfrac{ V_{immergé} }{ V_{tot} }$ la proportion du volume immergé par rapport au volume total.
Cette proportion vaut 89,5 %. On a donc que 89,5 % de l’iceberg se trouve sous l’eau.
Écoulement d’un fluide en régime permanent ; Débit volumique
I. Débit volumique
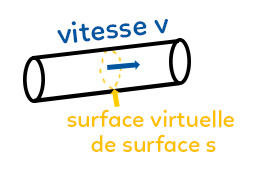
Le fluide s’écoule dans une canalisation représentée par le cylindre :
Pour définir le débit volumique, il faut d’abord s’imaginer une surface virtuelle à l’intérieur du cylindre et l’eau qui y passe à travers. Cette surface s’appelle la surface $S$ et à l’intérieur s’écoule un fluide à la vitesse $v.$ $Dv$ le débit volumique est le volume de fluide qui passe à travers la surface par unité de temps. Elle s’exprime en $m^3.s^{-1}.$
Par exemple, on a $Dv = 4m^3.s^{-1}.$ C’est-à-dire que $4 m^3$ de liquide s’écoule pendant une seconde.
La définition mathématique du débit volumique correspond à : $D_v = \dfrac{dV}{dt}$.
Le régime permanent c’est lorsqu’on a attendu suffisamment longtemps après avoir ouvert les vannes. Les effets de l’ouverture ont été transmis à la sortie de la canalisation. C’est l’inverse du régime transitoire car dans un régime transitoire, les effets de l’ouverture des vannes n’ont pas encore eu lieu de la même façon sur toute la canalisation. En effet, l’eau n’est pas encore arrivée à la sortie. En régime permanent, la vitesse reste constante sur toute la longueur de la canalisation. En régime permanent, on utilise la formule : $D_v = v \times S$, avec $Dv$ le débit volumique en $m^3.s^{-1}$, $v$ la vitesse de l’écoulement en $s^{-1}$ et $S$ la surface en $m^2.$
On adapte la formule en fonction du morceau de canalisation sur lequel on se situe.
II. Conservation du débit volumique
La conservation en physique c’est lorsque la grandeur reste constante. En régime permanent, sur une seconde, si à l’entrée du tuyau on a 5 m3 d’eau qui rentre, on a 5 m3 qui sort de l’autre côté. C’est la conservation du débit volumique. Le débit volumique est constant en tout lieu de la canalisation.
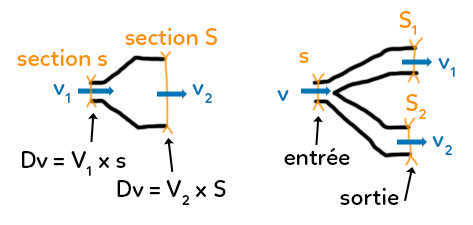
On a une canalisation qui s’élargit en sortie en une section $S$ beaucoup plus importante que la section $s$ de départ. On obtient alors $Dv = v_1\times s = v_2 \times S$, en régime permanent grâce à la conservation du débit.
Pour trouver $v_2$, on a : $v_2=v_1\times \dfrac{s}{S}$.
On voit alors que si la section à la fin s’agrandit, la vitesse à l’intérieur du tuyau va diminuer.
On peut aussi avoir une canalisation qui se sépare en deux autres canalisations. Le débit en entrée doit être égal à la somme des débits en sortie. En additionnant les deux volumes d’eau sortant des deux canalisations, on doit retrouver le même volume qu’au début.
Le débit volumique en entrée est de : $Dv = v\times s$.
En sortie on va les additionner : $Dv = v_1\times S_1 + v_2\times S_2$.
Alors : $v\times s = v_1\times S_1 + v_2\times S_2$, grâce à la notion de conservation de débit volumique.