Relation de Bernoulli
I. Ligne de courant
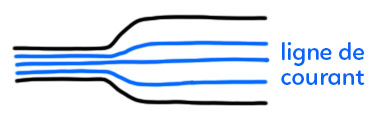
La ligne de courant est la trajectoire d’une particule de fluide. Le fluide est décrit comme un ensemble de particules de fluide.
Si on suit la trajectoire d’une particule dans le fluide, cela donne la trajectoire du courant. Cela va demander un effort d’intuition pour la deviner. Les bords noirs représentent une canalisation (petite au début et grande à la fin). Pour les particules de fluide, elles partent du milieu de la canalisation plus étroite, pour arriver au milieu de la canalisation plus large. De même, pour les autres particules, placées à différents endroits. Le tracé reste à intuitif puisqu’il est fait à main levée.
II. Relation de Bernoulli
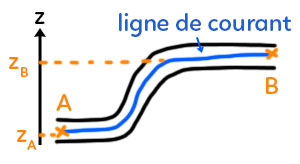
C’est une égalité qui va relier les caractéristiques de deux points d’une ligne de courant.
Voici un tuyau avec un point $A$ au début de la ligne de courant et un point $B$ en haut de la ligne. $A$ est à une altitude $z_A$ et $B$ à une altitude $z_B.$
La relation est la suivante : $p_A + \rho g z_A + \dfrac{1}{2}\rho v_A^2 + p_B + \rho g z_B + \dfrac{1}{2}\rho v_B^2$.
$p$ correspond à la pression en $A$ ou en $B$ (Pa), $\rho$ est la masse volumique du fluide ($kg.m^{-3}$), $g$ à l’intensité de pesanteur (m.s-2), $z$ à l’altitude du point $A$ ou $B$, $v$ à la vitesse du fluide au point d’intérêt $A$ ou $B$ (m.s-1).
Remarque : Lorsqu’un fluide est en contact avec l’air libre à pression $p0,$ le fluide est à la pression de l’air libre $p0.$
III. Application
On imagine un récipient avec un petit trou au fond (un point $B$). Le liquide va sortir par ce trou et le niveau du liquide va baisser. On doit calculer la vitesse à laquelle le liquide sort du point $B$. On a une hauteur $H$ d’eau et une section $S$ en surface et s au niveau du trou.
On a une ligne de courant et deux points $A$ et $B$. On connaît la pression en $A.$ On utilise alors la formule précédente : $p_A + \rho g z_A + \dfrac{1}{2}\rho v_A^2 + p_B + \rho g z_B + \dfrac{1}{2}\rho v_B^2$.
$A$ et $B$ sont tous les deux en contact avec l’air libre : $A$ car il est en surface et $B$ car l’eau s’écoule dans l’air : $pA = pB = p0.$
Il y a conservation du débit d’un fluide incompressible en régime permanent : $v_A \times S = v_B \times s$.
On veut trouver $v_A$ : $v_A = v_B \times \dfrac{s}{S}$.
On subsitue $v_A$ par cette expression dans la formule de départ, d’où : $\rho gH +\dfrac{1}{2} \rho v_B^2 (\dfrac{s}{S})^2 = \dfrac{1}{2} \rho v_B^2$.
On a alors : $v_B = \sqrt{\dfrac{2gHS^2}{S^2-s^2}}$
L'effet Venturi
I. Effet Venturi
C’est un effet en mécanique des fluides. Cela se produit lorsqu’il y a un rétrécissement de la zone de circulation d’un fluide. On prend un tuyau qui se rétrécit à un moment donné puis s’élargit de nouveau. Dans la partie où il est large, on appelle $S$ la section. C’est la surface si l’on coupe le tuyau. En $B,$ là où le tuyau est rétréci, la section s’appelle $s.$ On remarque tout de suite une ligne de courant qui passe par le milieu des sections.
1. Relation de Bernoulli
Sur la ligne de courant, on a : $\dfrac{1}{2} \rho v_A^2 + \rho g z_A + p_A = \dfrac{1}{2} \rho v_B^2 + \rho g z_B + p_B$
$v_A$ étant la vitesse d’une particule en $A,$
$\rho$ la masse volumique du fluide,
$g$ l’intensité de pesanteur,
$z_A$ l’altitude du point $A, $
$p_A$ la pression en $A.$
De même pour les valeurs associées au point $B.$
2. Conservation du débit
$S \times v_A = s \times v_B$. On isole $v_B$ : $v_B = \dfrac{S}{s} \times v_A$.
Or $S>s$ donc : $\dfrac{S}{s} >1$.
Cela signifie que $v_B >v_A$.
On a donc bien une accélération du fluide dans la zone de rétrécissement : c’est l’effet Venturi !
Par exemple, dans les montagnes, l’air qui arrive depuis la vallée vers le somment des montagnes a un large espace. Au moment de passer au-dessus de la montagne, son espace se rétrécit et donc le vent est beaucoup plus fort au sommet des montagnes qu’en bas.
II. Application à la trompe à eau
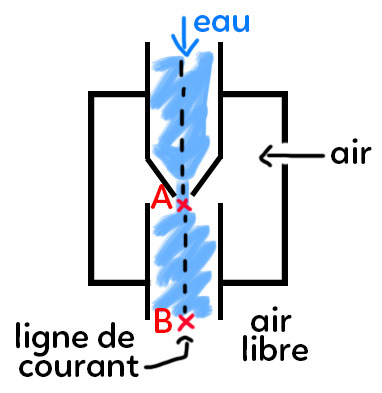
Le haut de la trompe à eau se branche au robinet et on allume le robinet. L’eau s’écoule dans la trompe à eau. Un côté peut être branché à une fiole à vide. L’eau s’écoule, l’air est aspiré et le vide se retrouvent dans la fiole à vide. La zone où circule l’eau se rétrécit : on a le point $A.$ Le point $B$ est situé en bas de la trompe à eau. La section $s$ contient $A,$ la section $S$ contient $B.$
L’air a la possibilité d’être en contact avec l’eau à un point situé près de $A.$ On retrouve la formation de bulles dans l’eau en dessous de la section $A$ car l’air y rentre. Une ligne de courant passe par $A$ et $B.$ En bas, l’eau est rejetée à l’air libre.
1. Relation de Bernoulli
Sur la ligne de courant, on chercher à isoler $p_A$ : $p_A = \dfrac{1}{2} \rho_{eau} (v_B^2 – v_A^2) + \rho_{eau} g (z_B-z_A) + p_B$.
On va faire l’hypothèse que le terme de droite est négligeable devant le terme de gauche : $\rho_{eau} g (z_B-z_A) << \dfrac{1}{2} \rho_{eau} (v_B^2 – v_A^2)$.
On a aussi la continuité des pressions en $B,$ au moment où l’eau est à l’air libre : $p_B = p_0$.
On peut alors remplacer dans l’équation : $p_A = \dfrac{1}{2} \rho_{eau} (v_B^2 – v_A^2) + p_0$.
2. Conservation du débit
On a $s\times v_A = S\times v_B$.
On isole $v_A$ : $v_A = \dfrac{S}{s} \times v_B$ d’où $p_A = \dfrac{1}{2} \rho_{eau} v_B^2 (1- (\dfrac{S}{s})^2) + p_0$.
Le rapport $\dfrac{S}{s}$ est plus grand que 1.
La parenthèse $(1- (\dfrac{S}{s})^2)$ sera négative.
La première partie de l’équation est donc négative. Par conséquent : $p_A <p_0$. $p_A$ est la pression en A et $p_0$ la pression de l’air.
La dépression va permettre d’aspirer l’air : c’est grâce à cela que l’air va se retrouver aspiré à l’intérieur donc la fiole va se vider et les bulles partent dans l’eau. C’est le principe de la trompe à eau.