Charge d'un condensateur
On sait qu’aux niveaux des armatures, des charges vont s’accumuler de part et d’autre.
I. Schéma
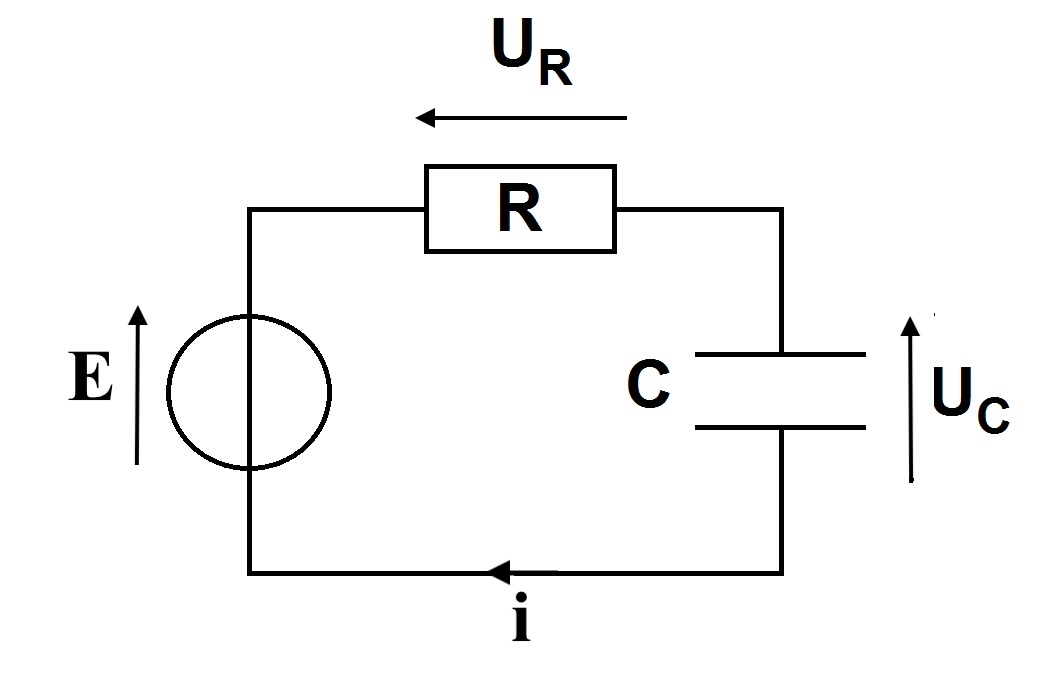
Voici le schéma de la charge d’un condensateur :
Il faut qu’il y ait un générateur de courant continu et de tension $E,$ une résistance et un condensateur, en série. Le courant est orienté dans le même sens que la tension du générateur (convention générateur). On représente en convention récepteur, le conducteur ohmique et le condensateur. Les flèches de tension à leurs bornes sont donc à l’opposé de celle du courant. La tension du conducteur ohmique s’appelle $U_R$ et celle du condensateur s’appelle $U_C$.
II. La loi des mailles
On utilise la loi des mailles dans ce circuit. On choisit un sens de rotation horaire. Quand on rencontre une flèche de tension dans le même sens que la rotation, on lui affecte un « + » et quand c’est en sens inverse on lui affecte un « – » . On aura alors : $E – U_R – U_C = 0$.
$U_R + U_C = E$ mais $R\times i +U_C = E$
Or $i = C\times \dfrac{dU_C}{dt}$.
D’où : $R\times C \times {dU_C}{dt} + U_C = E$.
Si on arrivait à trouver la solution d’une telle équation, on aurait $U_C$ en fonction du temps. On voudrait arriver à la forme canonique de l’équation. En divisant tout par $RC,$ on obtient cette équation : $\dfrac{dU_C}{dt} + \dfrac{u_C}{RC} = \dfrac{E}{RC}$
C’est une équation différentielle du premier ordre car on a une fonction inconnue $U_C$ mais aussi sa fonction par rapport au temps.
On pose alors $\tau = RC$. $\tau$ est le temps caractéristique.
On a alors l’équation : $\dfrac{dU_C}{dt} + \dfrac{u_C}{\tau} = \dfrac{E}{\tau}$ qui permet d’avoir accès en la résolvant à la fonction $U_C$ en fonction du temps.
III. Solution
La solution de cette équation est la suivante : $U_C(t) = E (1-e^{-t/\tau})$.
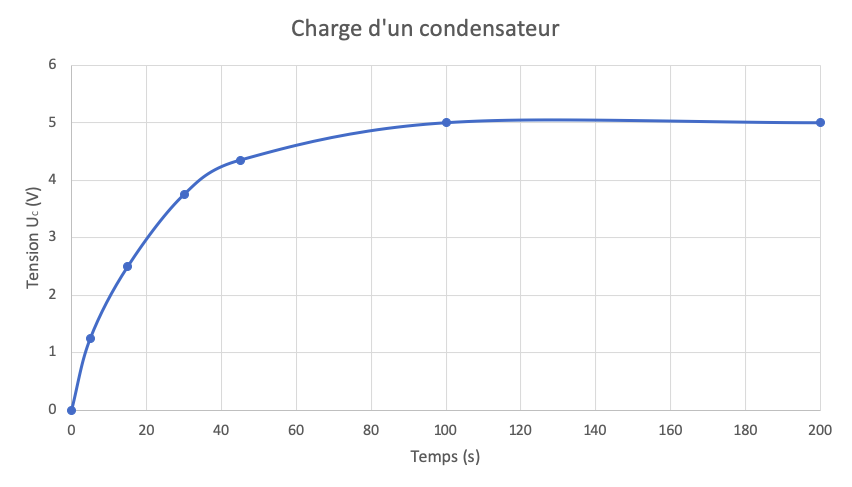
Graphiquement, si on trace cette fonction dans un repère avec $U_C$ en ordonnées et $t$ en abscisses, on obtient :
On obtient une courbe avec une certaine pente qui augmente puis se stabilise au fil du temps. Pour déterminer graphiquement $\tau$, on trace la tangente à la courbe à l’origine. Quand cette tangente coupe l’asymptote horizontale (E), on a $\tau$ sur l’axe des abscisses.
Plus la valeur de $\tau$ est petite, plus cela signifie que la charge aura lieu rapidement.
La tension $U_C$ à l’instant $\tau$ vaut $0,63\times E$ (sur l’axe des ordonnées).
Cela veut dire qu’à l’instant $t = \tau$, la tension du condensateur est à 63 % de sa valeur maximale. Cette première zone dans laquelle la tension évolue est appelée zone transitoire.
Puis, il y a une deuxième zone qui s’appelle régime permanent une fois que la tension est constante. A $5\tau$, $U_C$ a atteint 99 % de sa valeur finale $E.$
IV. Pourcentage de charge du condensateur
Le pourcentage de charge est : $\dfrac{q(t)}{q(t \rightarrow \inf)}$. Quand $t$ tend vers l’infini la charge est complète.
On peut aussi avoir : $\dfrac{C\times U_C(t)}{C\times U_C(t \rightarrow \inf)} = \dfrac{U_C(t)}{U_C(t \rightarrow \inf)}$.
C’est le pourcentage de charge à l’instant $t.$ Par exemple, si $t = \tau$ : $\% charge = \dfrac{0,63\times E}{E} = 0,63 = 63\%$.
Deux composants de base : le conducteur ohmique et le condensateur
I. Le conducteur ohmique
Parfois on l’appelle résistor ou résistance. L’idéal est plutôt résistor. Il y a un fil qui entre dans le conducteur ohmique et un autre qui en sort.
Il est traversé par un courant d’intensité $i$.
$u$ est la différence de potentiel aux bornes du conducteur ohmique.
Il est caractérisé par sa résistance $R$ en Ohms (Ω).
La relation courant-tension appelée aussi loi d’Ohm est la suivante : $ u(t) = R \times i(t)$.
II. Le condensateur
Deux barres représentent des armatures (rectangles métalliques). Il y a un fil qui arrive sur la première armature et un autre fil qui sort de la deuxième armature. Au milieu, il y a un isolant caractérisé par un coefficient (F.m-1). À cause de cet isolant, les électrons ne vont pas pouvoir passer. Le courant va de gauche à droite donc les électrons sont dans le sens inverse.
Comme les électrons ne peuvent pas passer de l’autre côté de l’armature, ils s’accumulent sur la première. Par conséquent, on trouve une charge négative $-q$ sur l’armature où s’accumulent les électrons. Sur l’autre armature, il va y avoir un manque d’électrons. Cela va donner une charge positive $q$ sur l’armature. L’ensemble des armatures est neutre.
La distance entre les deux plaques est notée $e.$
Le condensateur est caractérisé par sa capacité $C.$
Il existe une formule qui permet de déterminer cette capacité $C$ : $C = \epsilon \times \dfrac{S}{e}$, avec :
$C$ la capacité en F,
le coefficient en F.m-1,
$S$ la surface des armatures en m2,
$e$ la distance entre les armatures en m.
La charge emmagasinée sur une armature est égale à : $q = C \times u$.
Plus le condensateur a une capacité importante, plus il est capable d’accumuler des électrons. Cela permet d’accumuler de l’énergie électrique. Une fois qu’un condensateur est rempli, les électrons veulent repartir et circuler et donc libérer de l’énergie.
Pour les anciens flashs d’appareil photo, avant que le flash ne se déclenche, le condensateur se chargeait et quand on appuyait sur le bouton, le condensateur se déchargeait rapidement dans une petite lampe. Ce qui provoquait l’éclat du flash.
La relation courant-tension est à connaître par cœur : $i = \dfrac{dq}{dt}$ et $q = C\times u$.
On a aussi : $i = C \times \dfrac{du}{dt}$.
Décharge d'un condensateur
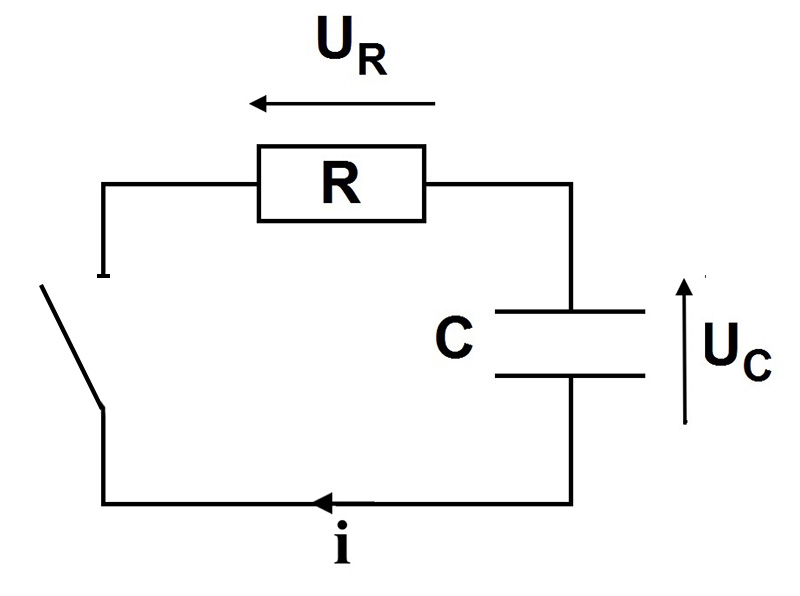
I. Schéma
On dit que le condensateur est chargé lorsqu’à ses bornes il existe déjà une tension. Cette tension est notée $E.$
A $t = 0^-$ (juste avant $t = 0), u_c = E$.
A $t = 0,$ on ferme l’interrupteur donc le circuit.
Tant que l’interrupteur est ouvert, le courant ne peut pas circuler. Puisque le condensateur est chargé, il va alors se décharger. Comment ?
II. Loi des mailles
On a choisi de tourner dans le sens anti-horaire dans la maille. On a alors : $u_c + u_R = 0$.
Selon la loi d’Ohm : $u_R = R\times i$.
Donc $u_c + R\times i = 0$.
Dans le cas d’un condensateur : $i = C\dfrac{du_c}{dt}$.
On remplace dans l’équation : $u_c+RC\dfrac{du_c}{dt} = 0$. On a une équation différentielle.
On divise toute l’équation par RC : $\dfrac{du_c}{dt} + \dfrac{u_c}{\tau} = 0$, avec $RC = \tau$.
$\tau$ est la constante de temps ou temps caractéristique (s). (E) est une équation différentielle du premier ordre. Comment connaît-on l’unité de $\tau$ ?
$\dfrac{du_c}{dt}$ sont des volts sur des secondes donc $\dfrac{u_c}{\tau}$ doit être dans les mêmes unités. $\tau$ est bien un temps.
III. Solution
La solution de l’équation différentielle est toujours du même type : $u_c(t) = Ae^{-t/\tau}$, avec $A$ une constante à déterminer. On utilise les conditions initiales.
A $t = 0,$ la tension aux bornes du condensateur est égale à $E.$
Mais aussi, à $t = 0,$ $u_c(0) = A$.
D’où $u_c(t) = Ee^{\frac{-t}{\tau}}$. En traçant la courbe, on a une exponentielle décroissante.
On peut trouver $\tau$ en traçant la tangente à l’origine.
$\tau$ correspond au croisement avec l’axe des abscisses. A cet instant $\tau$, la valeur de $u_c$ vaut 0,37E, donc 37 % de la tension initiale. Entre $t = 0$ et $5\tau$, on appelle cela le régime transitoire et entre $5\tau$ et l’infini, le régime permanent. On va alors considérer qu’il ne se passe plus rien et que la tension est fixe.