Vitesse, distance & temps
Vitesse, distance et temps
La vitesse, la distance et le temps sont reliés par une formule, à connaitre par coeur :
$V=\dfrac{D}{T}$.
La vitesse est donc égale à la distance divisée par le temps.
Exemple
En voiture, on roule par exemple à $40$ km/h, on effectue donc le rapport de la distance (kilomètres) par le temps (heure).
Calculs de vitesses, temps ou distances
1) Dans certains cas, on peut être amené à calculer la distance parcourue pendant un temps donné à une vitesse donnée.
Il faut donc isoler $\text{D}$ dans la formule, en utilisant l’égalité des produits en croix et en se rappelant que $\text{V} = \dfrac{\text{V}}{1}$.
On obtient alors que
$\text{D} \times 1 = \text{D} = \text{V} \times \text{T}$.
La distance est donc égale au produit du temps par la vitesse
Il est conseillé de ne pas apprendre par coeur cette formule, pour ne pas se tromper, mais plutôt de connaitre la démarche permettant de la retrouver à partir de la formule de la vitesse.
2) On peut aussi calculer le temps en connaissant la vitesse et la distance.
On obtient alors $\text{T} = \dfrac{\text{D}}{\text{V}}$.
Le temps est égal à la distance divisée par la vitesse.
Enfin, il faut avoir une cohérence des unités pour ne pas obtenir un mauvais résultat.
Il existe différentes unités pour mesurer une distance (mètre, kilomètre,…) de même que pour le temps (seconde, heure,…).
Le choix effectué pour les unités de la distance et du temps impose l’unité de la vitesse.
De même, si on choisit l’unité de la vitesse, les unité du temps et de la distance sont imposées.
| Unité Vitesse | Unité Distance | Unité Temps |
| km/h | kilomètre | heure |
| m/s | mètre | seconde |
Exemples :
1) Une voiture roule à 45 km/h. Quelle distance aura-t-elle parcouru en deux heures ?
Ici, on connaît la vitesse et le temps, on cherche donc la distance.
En appliquant la même démarche que dans le cours, on trouve que :
$\text{D} = \text{V} \times \text{T}$.
L’unité de la vitesse est km/h et l’unité du temps est l’heure, la cohérence est respectée : la distance sera exprimée en kilomètres.
$\text{D} = 45 \times 2 = 90$ km.
2) Un cycliste parcourt 2 kilomètres en 15 minutes. Quelle est sa vitesse en km/h ?
La vitesse est donnée par la formule $\text{V} = \dfrac{\text{D}}{\text{T}}$.
On souhaite exprimer la vitesse en km/h. Il faut donc convertir 15 minutes en heure.
Or 15 minutes correspondent à un quart d’heure.
Ainsi,
$\text{V} = \dfrac{2}{\dfrac{1}{4}} = 8$km/h.
3) La lumière possède une vitesse de $V = 3 \times 10^8$ m/s. La distance Soleil-Terre vaut $D = 150 \times 10^6$ km.
Quel temps faut-il à la lumière pour arriver à la surface de la Terre ?
La formule est
$\text{T} = \dfrac{\text{D}}{\text{V}}$.
On doit convertir la distance en mètre car la vitesse est donnée en m/s.
Ainsi, $D = 150 \times 10^9$ m.
On trouve alors
$\text{T} = \dfrac{150 \times 10^9}{3 \times 10^8} = 500$s.
Or 60 secondes sont égales à une minute, par produit en croix on trouve donc que
$\text{T} = 500 \times {1} \div 60 \approx 8$ min.
Conversions heures décimales / heures minutes
Conversions heures décimales / heures minutes
Introduction
Afin de comprendre le sujet, considérons un exemple.
Un trajet en voiture dure 3h. Au milieu du parcours, le conducteur décide de faire une pause. Combien de temps a-t-il roulé ?
Instinctivement, on répond qu’il a roulé pendant 1h30.
Pourtant, lorsque l’on effectue le calcul $3 \div 2$ on trouve $1,5$.
Le dernier calcul donne un résultat en heures décimales alors que l’on exprime habituellement le résultat en heures minutes.
Définition
Pour passer d’une unité à l’autre, il faut se souvenir qu’il y a proportionnalité entre les heures décimales et les minutes, avec un coefficient de proportionnalité égal à 60 : 1 heure décimale correspond à 60 minutes.
| heures décimales | 1 | 1,5 |
| minutes | 60 | 90 |
Or 1 heure vaut 60 minutes, donc 90 minutes valent bien 1 heure et 30 minutes.
Exemple :
On vient d’effectuer un trajet de 260 km en 2h15 min. On se demande quelle était notre vitesse moyenne.
Pour cela, on utilise la formule
$\text{V} = \dfrac{\text{D}}{\text{T}}$.
Pour les calculs, il faut convertir les heures minutes en heures décimales.
On utilise donc à nouveau un tableau de proportionnalité mais il faut d’abord penser à convertir les heures minutes en minutes.
Or 2 heures correspondent à 120 minutes, ainsi 2h15min valent 135 minutes.
Enfin, pour trouver le résultat en heures décimales, on divise 135 par 60.
| heures décimales | 1 | 2,25 |
| minutes | 60 | 135 |
Ainsi,
$\text{V} = \dfrac{260}{2,25} \approx 116$ km/h.
Conversions volumes mètres cube & litres
Conversions de volumes en mètres cube et litres
Unités usuelles
Pour mesurer un volume, deux unités peuvent être utilisées.
Il existe un système de mesure international qui est le mètre cube et un système utilisé davantage au quotidien, le litre.
La relation à connaitre par coeur entre les deux est : 1 L = 1 dm$^3$.
Un litre correspond donc au volume contenu dans un cube d’un décimètre de côté, c’est à dire 10 cm.
Remarques
Dans le tableau des longueurs, une unité correspondait à une colonne.
Dans le tableau des aires, une unité correspondait à deux colonnes.
Pour le tableau des volumes, une unité correspond à trois colonnes.
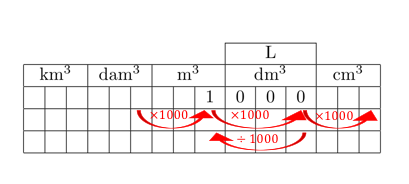
Conversions d’unités de volumes
Lorsque l’on souhaite convertir par exemple 1m$^3$ en litre, on commence par écrire le 1 des unités dans la colonne de droite liée au $m^3$.
On remplit enfin le tableau avec des $0$ jusqu’à arriver à la dernière colonne correspondant aux litres, ou encore aux décimètres cube.
On obtient 1m $^3 = $ 1000 dm$^3$, c’est à dire 1m $^3 = $ 1000 L.
On peut aussi retenir que pour passer des mètres cube aux décimètres cube, il faut multiplier par 1000, et pour passer des décimètres cube aux mètres cube, on divise par 1000.
Exemple :
On sait que 1 litre est égal à 1000 millilitres, or 1 litre est aussi égal à 1000 centimètres cube, donc 1 mL = 1 cm$^3$.
Les préfixes de nano à giga
Les préfixes de nano à giga
Ces dix préfixes sont à connaitre par coeur.
On part de l’unité qui vaut $10^0 = 1$ et on regarde différentes puissances de $10$.
| Préfixe | Symb | Puissance ($10^n$) | Exemple |
| Giga | G | $10^9 = 1 000 000 000$, un milliard | GigaOctet(taille d’un film numérique) |
| Méga | M | $10^6 = 1 000 000$, un million | MegaOctet (Image, Photo) |
| Kilo | k | $10^3 = 1 000$, mille | $1$ kg de … |
| Hecto | h | $10^2 = 100$ | 1 hL $=$ 100 L |
| Déca | da | $10^1 = 10$ | 1 dam = 10 m; décathlon (10 épreuves) |
| $10^0 = 1$ | UNITE | ||
| Déci | d | $10^{-1} = 0,1$, un dixième | 1 dg = 0,1 g |
| Centi | c | $10^{-2} = 0,01$, un centième | 1 cL = 0,01 L; centimes |
| Milli | m | $10^{-3} = 0,001$, un millième | 1mm = 0,001 m |
| Micro | $\mu$ | $10^{-6} = 0,000 001$, un millionième | $1\mu$m = 0,000 001m = 1 micron |
| Nano | n | $10^{-9} = 0,000 000 001$, un milliardième | 1 nm, étude de l’atome, nanotechnologie |