Rotations
Rotations
Rotations
Définition
Les rotations sont des transformations du plan. Une rotation est définie par une centre $O$ et un angle $\alpha$ exprimé en degré.
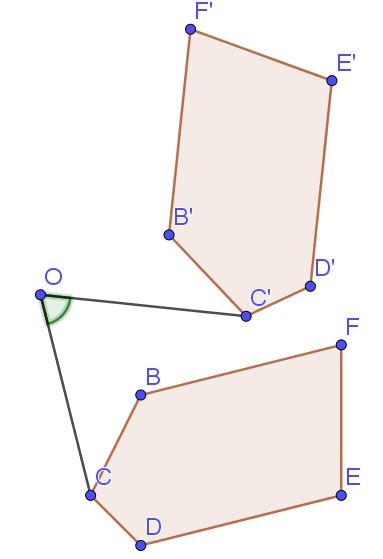
Pour chaque point de $BCDEF$ on pourra écrire :
$OC = OC’$
$\widehat{COC’} = \alpha$
Exemple :
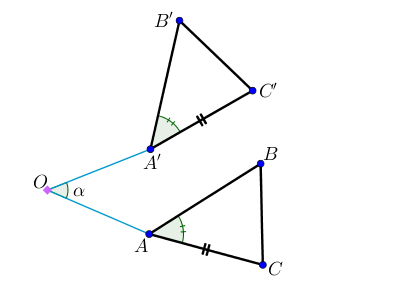
On considère la rotation de centre $O$ et d’angle $\alpha = 45°$. La rotation s’effectue dans le sens contraire des aiguilles d’une montre.
Pour construire l’image de $A$ par la rotation, on utilise les relations suivantes :
$OA = OA’$
$\widehat{AOA’} = 45°$
Propriétés :
Les rotations conservent :
– les longueurs
– les aires
– les mesures d’angles
La figure n’est pas déformée.