Médiatrice d’un segment
Médiatrice d’un segment
I – Quelle est la définition de la médiatrice d’un segment ?
La médiatrice d’un segment est la droite perpendiculaire à ce segment passant en son milieu.
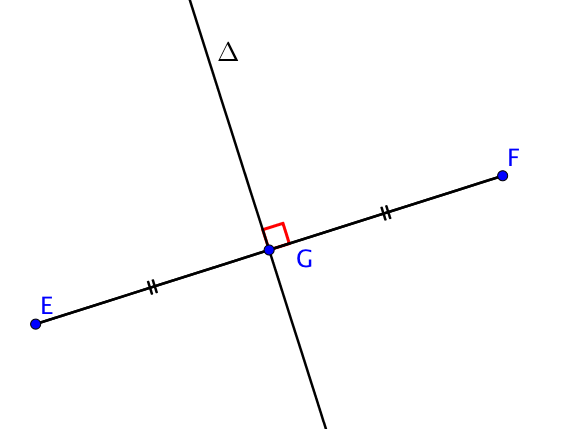
On considère le segment $[EF]$ et $G$ son milieu.
La droite $\Delta$ perpendiculaire à $[EF]$ passant par $G$ est donc la médiatrice de $[EF]$.
II – Quelles sont les propriétés de la médiatrice d’un segment ?
1) Si un point $M$ appartient à la médiatrice d’un segment, alors ce point $M$ est équidistant des extrémités de ce segment.
Exemple :
Soit $M$ un point de $\Delta$, alors $M$ est équidistant (à la même distance) des extrémités de $[EF]$, c’est-à-dire de $E$ et de $F$.
Cela revient donc à écrire que $ME = MF$.
2) Si un point $M$ est équidistant des extrémités d’un segment, alors ce point $M$ appartient à la médiatrice de ce segment.
La deuxième propriété est la réciproque de la première. Cela signifie que l’on inverse le « si » et le « alors » de la propriété précédente.
Exemple :
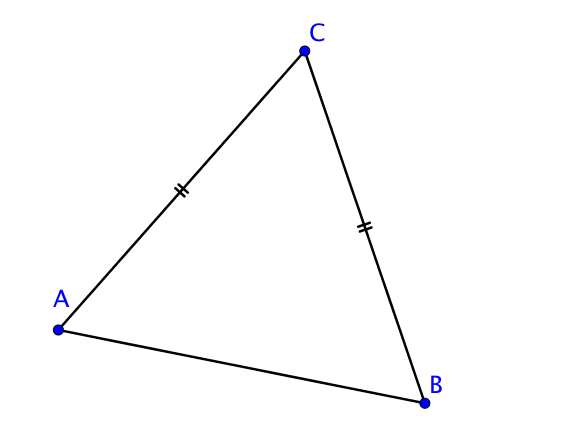
Soit $[AB]$ un segment et $C$ un point tel que le triangle $ABC$ soit isocèle en $C$.
Cela signifie que $CA = CB$.
Ainsi, le point $C$ est équidistant de $A$ et $B$ ou encore $C$ est équidistant des extrémités du segment $[AB]$.
Donc, $C$ appartient à la médiatrice du segment $[AB]$.
III – Construction au compas
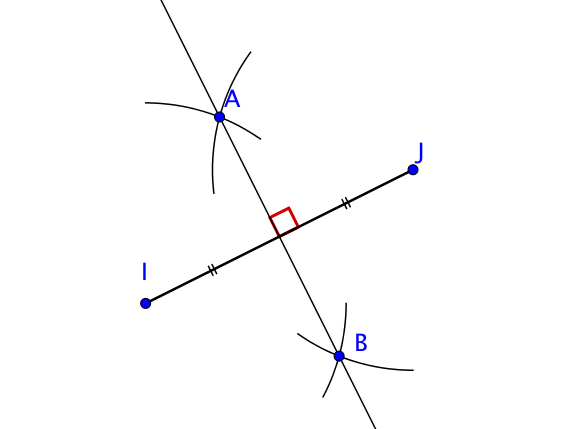
On souhaite désormais construire la médiatrice du segment $[IJ]$.
On utilise uniquement le compas et la règle non graduée en utilisant les propriétés précédentes.
Pour se faire, on trace un point $A$ équidistant des extrémités du segment puis un deuxième $B$. Ces deux points appartiennent donc à la médiatrice du segment. En les reliant, on obtient la médiatrice du segment $[IJ]$.
Elle passe donc par le milieu de $[IJ]$ et est perpendiculaire à ce dernier.