Angles alternes-internes
Angles alternes internes
I) Définition
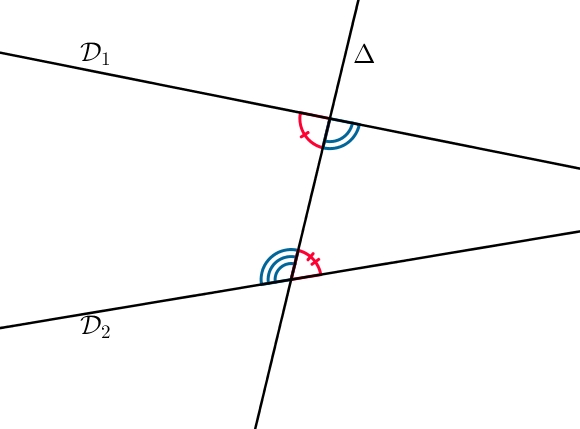
On considère deux droites $\mathcal{D}_1$ et $\mathcal{D}_2$ et une droite $\Delta$ sécante aux deux autres droites.
Il est alors possible de définir deux couples d’angles alternes-internes (de même couleur sur la figure).
On utilise le terme alterne pour indiquer que les angles sont de part et d’autre de la droite sécante et interne pour signifier que les angles sont compris entre les droites $\mathcal{D}_1$ et $\mathcal{D}_2$.
Exemple :
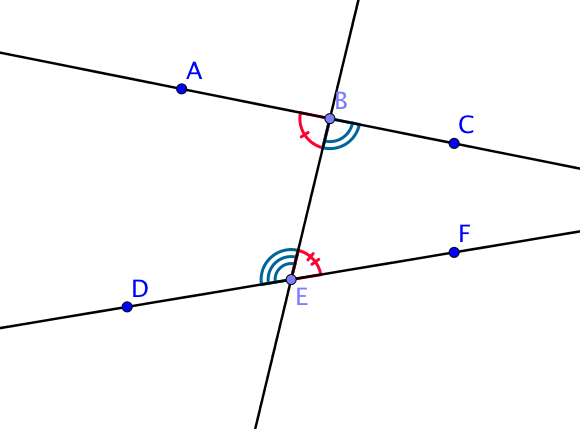
Dans ce cas, les couples d’angles alternes-internes sont
- $(\widehat{ABE}, \widehat{BEF})$
- $(\widehat{EBC}, \widehat{DEB})$
II) Propriétés
1 ) Si les deux droites $(AC)$ et $(DF)$ formant les angles alternes-internes sont parallèles alors les angles alternes-internes sont égaux.
Exemple :
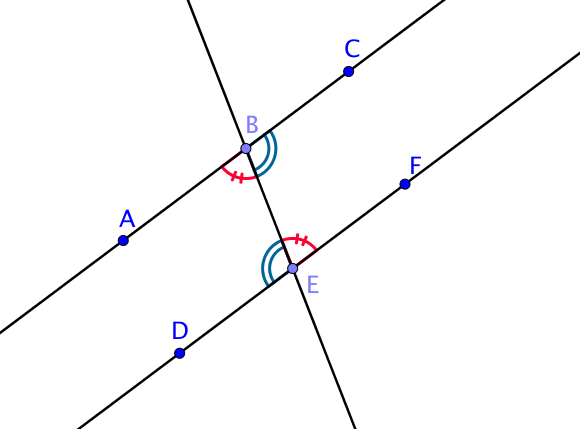
Si on sait que $(AC)//(DF)$, alors les angles alternes internes sont égaux c’est à dire :
- $\widehat{ABE}= \widehat{BEF}$
- $\widehat{EBC} = \widehat{DEB}$
2 ) Si les angles alternes internes sont de même mesure, alors les droites $(AC)$ et $(DF)$ sont parallèles.
Si $\widehat{ABE}= \widehat{BEF}$, alors les droites $(AC)$ et $(DF)$ sont parallèles.