Repérage dans le plan

Repérage dans le plan

Repérage dans le plan

Définition : repère et coordonnées

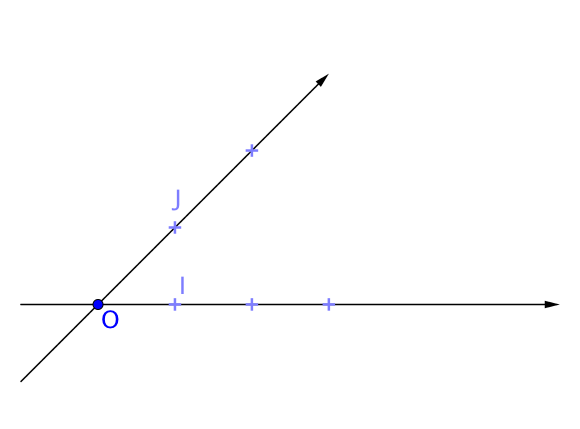
Pour repérer un point dans un plan, on utilise un repère, c’est à dire deux axes ayant la même origine $O$.

Chaque axe dispose d’une unité, qui peut être différente, et est gradué en reportant plusieurs fois cette unité.

Le repère s’appelle alors $(O, I, J)$.

Le premier axe correspond à l’axe des abscisses et le second à l’axe des ordonnées. 

Au collège, on se limite au cas où les deux axes sont perpendiculaires. On parlera alors de repère orthogonal.

Si les unités des deux axes sont égales, on dira qu’il s’agit d’un axe orthonormal ou orthonormé. 

L’axe horizontal correspond à l’axe des abscisses. Les abscisses permettaient de repérer les points sur la droite graduée.
L’axe vertical correspond à l’axe des ordonnées. 

Pour repérer un point dans le repère, on utilise deux nombres

Lire les coordonnées d’un point

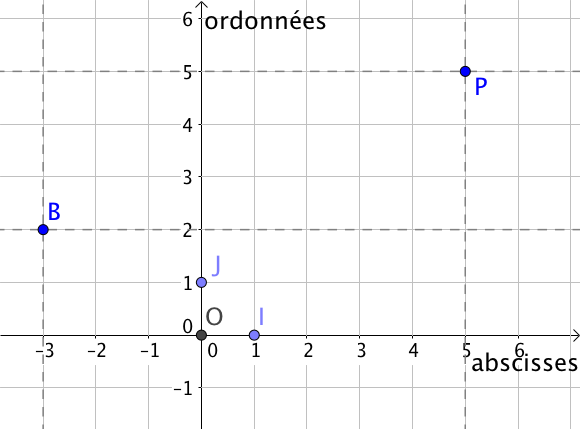
a) On cherche les coordonnées du point $P$.

Pour cela, on trace une droite perpendiculaire à l’axe des abscisses passant par $P$. Le point d’intersection entre ces deux droites correspond à l’abscisse du point $P$. L’abscisse de $P$ vaut $5$

On trace de même une droite perpendiculaire à l’axe des ordonnées passant par $P$ pour lire l’ordonnée du point. L’ordonnée de $P$ vaut aussi $5$.

Finalement, on a $P(5; 5)$. Le couple $(5; 5)$ est les coordonnées du point $P$. 

b) De même, on cherche les coordonnées du point $B$.

On a $B(-3; 2)$. 

Placer un point dans un repère

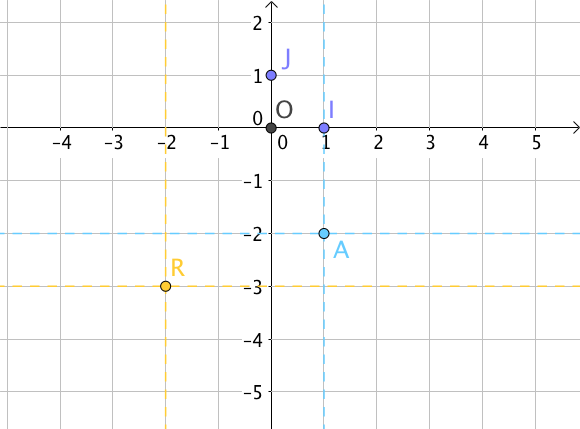
Plaçons le point $A(1; -2)$.

On trace alors la perpendiculaire à l’axe des abscisses passant par $1$ puis la perpendiculaire à l’axe des ordonnées passant par $-2$ : le point $A$ se situe à l’intersection des deux droites. 

On place de la même façon le point $R(-2; -3)$.