Fonction cube

Fonction cube

Fonction cube

Définition

La fonction cube est une fonction définie sur $\mathbb{R}$ à valeurs dans $\mathbb{R}$ et se note $\left \{ \begin{array}{ccccc} f & : & \mathbb{R} & \to & \mathbb{R} \\ & & x & \mapsto & x^3 \end{array} \right.$.

Variations

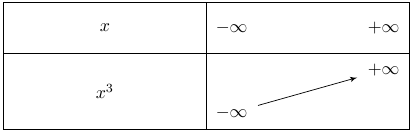
Cette fonction est strictement croissante pour tout réel $x$.

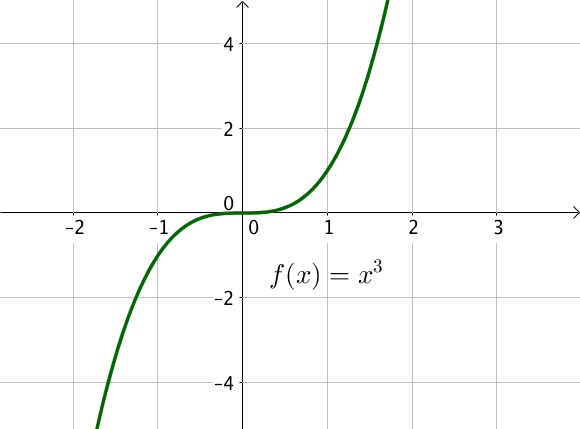
La représentation graphique de la fonction cube est la suivante :

A retenir :

Pour tout $x \geq 0, \ x^3 \geq 0$

Pour tout $x \leq 0, \  x^3 \leq 0$. 

Les fonctions $u$ et $u^3$ ont les mêmes variations. 

Par exemple, pour étudier les variations de $(x+3)^3$, on peut étudier les variations de $x + 3$ puis en déduire celle de $(x+3)^3$.

Or on sait que $x + 3$ est une fonction croissante sur $\mathbb{R}$, ainsi, $(x+3)^3$ est aussi une fonction croissante.

Pour tous réels $a$ et $b$, 

$a^3 – b^3 = (a – b)(a^2 + ab + b^2)$.