Arguments historiques et calculs de l'âge de la Terre
Arguments historiques et calculs de l’âge de la Terre
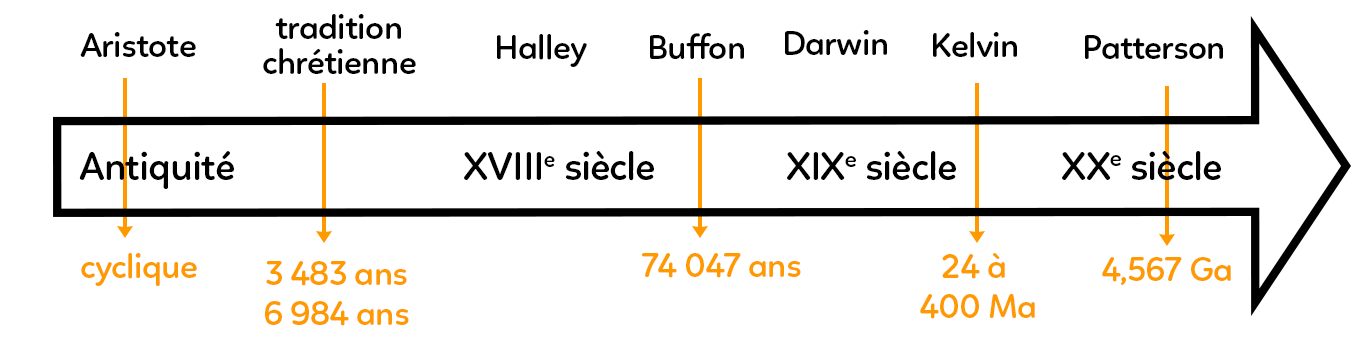
Au cours du temps, comment a-t-on appréhendé l’âge de la Terre ? Aujourd’hui, l’âge de la Terre fait l’unanimité : 4,567 giga années (milliard d’années).
I. Antiquité et tradition chrétienne
On peut remonter très loin chez les philosophes grecs, dès Aristote, quatre siècles avant notre ère. Il faut considérer qu’il y avait une vision totalement cyclique des événements, c’est-à-dire qu’il n’y avait ni commencement, ni fin. Donc l’âge de la Terre ne suscitait aucune question, aucune problématique. Pas de début, pas de fin, donc pas d’âge.
Les ouvrages et les lectures bibliques vont amener à une réflexion, une estimation, un calcul d’âge qui était autour de 3 483 ans à 6 984 ans. Cette tradition chrétienne a perduré très longtemps.
II. XVIIIe siècle
Il faut attendre le XVIIIe siècle, le siècle des Lumières avec le début du développement des sciences et la naissance de la géologie, pour reprendre des calculs et trouver par différents géo chronomètres l’âge de la Terre.
Les géochronomètres c’est utiliser la géologie, donc les sciences qui étudient la Terre et ses différentes enveloppes, pour essayer d’appréhender son âge.
A. Salinité des mers
On peut notamment citer, au début du XVIIIe siècle, Edmond Halley qui a travaillé sur la salure et la salinité des mers. Au XVIIIe siècle, c’est l’approche empirique (observation) qui prévaut. On observe la nature, les roches et à partir de ces observations, on expérimente. Edmond Halley observe que l’eau de mer est salée, elle contient du NaCl. Son constat est que ce NaCl provient de l’érosion des montagnes. En calculant la quantité de NaCl qui est chaque année érodée de la montagne vers la mer et en postulant qu’initialement, au moment où la Terre s’est formée, l’eau des océans était douce, (il connaît la masse des océans actuels, il connaît la quantité NaCl apporté de la montagne à la mer) il en déduit un âge. Il va estimer un âge de l’ordre de la centaine de milliers d’années, c’est beaucoup plus important que l’âge biblique mais on reste quand même loin de la réalité.
B. Stratigraphie
Comme géochronomètre, on peut également citer la stratigraphie. C’est quand les sédiments se posent dans un milieu aqueux de manière horizontale. Lorsqu’on regarde une falaise, on observe des strates qui correspondent à des peaux sédimentaires. Si on a une idée de la hauteur de la falaise, par exemple 130 mètres, alors on a une idée de la vitesse de sédimentation, par exemple au niveau d’un estuaire c’est facile à mesurer : à peu près à 0,1 millimètre par an.
On peut utiliser la formule $v = dfrac{d}{t}$.
Pour une falaise de 130 mètres ($d$) et une vitesse de dépôt de 0,1 millimètre par an ($v$), on cherche l’âge, soit $t$ donc on isole $t$ dans la formule suivante : $v = dfrac{d}{t}.$
Le $t$ vaut l’épaisseur de la falaise divisée par une vitesse : $t = dfrac{d}{v}.$
Si cette vitesse est de 0,1 millimètre par an, le calcul se fait assez simplement, l’âge est donc de 1 300 000 ans. On est très loin de l’âge proposé jusqu’alors.
Ce géo chronomètre qui utilise la stratigraphie a été utilisé par Buffon ou encore Darwin.
C. Temps de refroidissement de la Terre
Buffon a envisagé une méthode de calcul de l’âge de la Terre avec une approche expérimentale extrêmement rigoureuse de géo chronomètre qui était le temps de refroidissement de la Terre. Il a hérité de forges en Bourgogne, et au sein de ses forges, il a pris des boulets de diamètres variables en fer, les a chauffés, et a mesuré le temps qu’il fallait pour que le boulet soit touchable 1 seconde, avec des tailles de boulets variables. Il a constaté que plus le boulet de fer très chaud est grand, plus le temps de refroidissement est long. Ensuite, il a également mesuré le temps pour lesquels ces boulets de diamètres variables revenaient à la température actuelle. Connaissant le diamètre de la Terre, il a extrapolé ses résultats pour avoir une idée du temps de refroidissement de notre planète. Il est arrivé à un âge de 74 047 ans, très précis, même si celui-ci n’était pas du tout significatif étant donné l’incertitude qu’il y avait. Il y a beaucoup de paramètres qu’il n’intégrait pas. La Terre n’est pas du fer mais un ensemble d’enveloppes concentriques de composition différentes. Ensuite, il n’a pris en compte qu’une transmission par conduction. Et enfin, la Terre continue d’émettre de la chaleur au niveau du manteau inférieur sous forme de radioactivité, donc il y a encore de la chaleur interne dans notre globe terrestre qui est émise. Il y a aussi d’autres formes d’émission.
II. XIXe siècle
Darwin a travaillé au niveau de la stratigraphie et a constaté qu’au sein d’une strate sédimentaire, il y avait une homogénéité des fossiles. Or son approche évolutive est que l’évolution des espèces est relativement longue. Si au sein d’une strate sédimentaire on a toujours les mêmes fossiles (ammonite ou autre), cela veut dire que, comme il y a beaucoup de strates sédimentaires, l’âge de la Terre n’est pas de l’ordre de la centaine d’années mais plus du million d’années.
Kelvin reprend un peu l’idée de Buffon, mais en prenant en compte la loi de Fourrier sur le temps de refroidissement. La loi de Fourrier intègre la température en fonction du temps dans les trois dimensions de l’espace. Lord Kelvin va trouver un âge de la Terre avec le centre chaud et la surface plus froide, de 24 à 400 millions d’années. Son travail omet le fait qu’il n’y a pas que de la conduction comme transfert thermique mais qu’il y a aussi de la convection. Il omet également la chaleur permise par désintégration radioactive, il ne connaissait pas la radioactivité. Mais là encore, on approche de plus en plus du chiffre maintenant accepté.
III. XXe siècle
Pour obtenir un chiffre consensuel de l’âge de la Terre, faut attendre le XXe siècle et la datation absolue par la loi des croissances radioactives. Clair Patterson propose en 1957 grâce à un couple d’éléments radiogéniques (l’uranium qui donne l’élément plomb) un âge de la terre de 4,567 giga années.
Évaluation actuelle de l'âge de la Terre - Partie 1
Évaluation actuelle de l’âge de la Terre – Partie 1
I. Rutherford et les principes de la datation radioactive (datation absolue)
La datation radioactive a été mise en place à la suite de la découverte de la radioactivité en 1896 par Becquerel. Ces principes de datation ont été principalement mis en place par Rutherford grâce aux travaux de Pierre Curie. Ces essais datent du début du XXe siècle. Avec la découverte de la radioactivité naturelle, Rutherford a compris que la Terre émettait de la chaleur parce qu’elle en produisait et non plus seulement parce qu’elle se refroidissait.
Cela a remis en question les datations de la Terre sur le temps qui se serait écoulé depuis le début du refroidissement de la Terre. Le fait que la Terre produise de la chaleur par radioactivité remet donc la datation en question.
Loi de décroissance radioactive exponentielle
Rutherford a mis au point une nouvelle technique de datation en utilisant la radioactivité. Elle repose sur l’élément de base qui est la désintégration d’éléments isotopes radioactifs. Ces éléments radioactifs instables dans la nature sont appelés pères. Ils sont capables de se désintégrer de façon spontanée en éléments fils.
L’élément fils est alors appelé radiogénique : il est stable. Cette désintégration se fait de façon naturelle au sein de la Terre et est alors source d’un rayonnement, source de chaleur. La Terre émet de la chaleur par désintégration radioactive de certains de ses éléments.
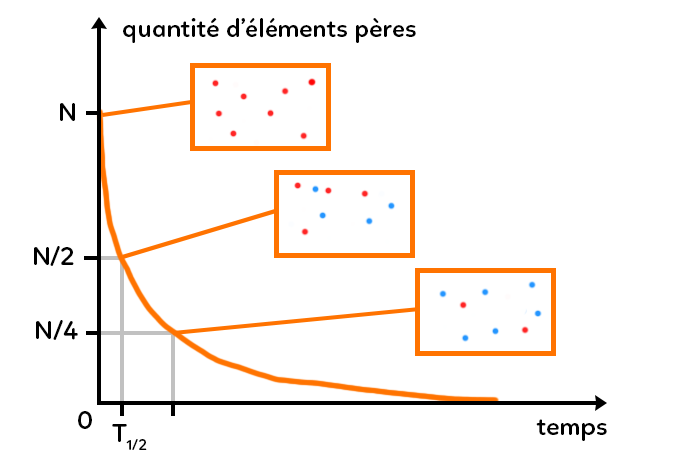
On peut donc dire que la désintégration radioactive va donc suivre certaines propriétés. On parle de loi de décroissance radioactive exponentielle. Graphiquement, cela se traduit par une courbe décroissante (orange) montrant l’évolution de la quantité d’élément pères par rapport au temps. Elle a une forme typique de fonction exponentielle.
Concrètement, si on s’intéresse à la quantité d’élément pères avec $N$ la quantité d’éléments pères au début de l’expérience, on peut observer que la quantité diminue au cours du temps avec une certaine propriété. Si on s’intéresse au temps qu’il faut pour diminuer de moitié la quantité initiale de pères par deux, on voit que le temps associé à ce moment s’appelle le temps $T_{1/2}$ ou temps de demi-vie. On parle parfois aussi de période radioactive.
La demi-vie est le temps qu’il faut pour qu’un stock d’éléments radioactifs se désintègre pour moitié. Ce temps ne dépend pas du stock de départ donc quelle que soit la quantité de pères au départ, il faudra toujours le même temps (demi-vie) pour diviser ce stock par deux.
Si on attend encore une demi-vie, on a $N$ divisé par 2 donc $N/4.$ A ce moment, on a diminué le stock d’élément encore par deux. Au bout de deux demi-vies, on a donc diminué le stock de départ par quatre.
La fonction qui traduit la disparition de l’élément père peut se noter : $P = P_0 e^{-lambda t}$
Avec $P_0$ la quantité au départ et $lambda$ la constante de désintégration radioactive.
Cette constante vaut : $lambda = dfrac{ln2}{T_{1/2}}$
Cette loi de désintégration radioactive va pouvoir s’appliquer à plusieurs éléments que l’on retrouve sur Terre.
Exemples
Le carbone 14 (14C) est un élément radioactif qui va se désintégrer en azote 14 (14N). La demi-vie du carbone 14 est de 5 730 ans, ce qui est assez court. Il est principalement utilisé pour dater des fossiles.
En revanche, l’Uranium, dont il existe deux isotopes radioactifs 235U et 238U, qui se désintègrent spontanément en 207Pb et en 206Pb, va avoir un temps de demi-vie beaucoup plus grand, de l’ordre du milliard d’années.
235U a une demi-vie de l’ordre de 0,7 milliard d’années.
238U a une demi-vie de l’ordre de 4,47 milliards d’années.
II. Dater l’âge de la Terre
Ces éléments radioactifs peuvent être utilisés pour dater des objets et en l’occurrence, on va essayer de dater l’âge de la Terre.
Grâce à la loi de désintégration radioactive, on peut appliquer cela à des roches trouvées sur Terre. Le problème, c’est qu’il faut que la roche ait conservé ses éléments, qu’elle n’en ait pas perdu au cours du temps, ce qui fausserait la détermination du nombre d’éléments qu’on pourrait y trouver et donc l’âge calculé.
On a besoin d’échantillons très particuliers et les roches continentales subissent beaucoup d’érosion et perdent certains de leurs éléments.
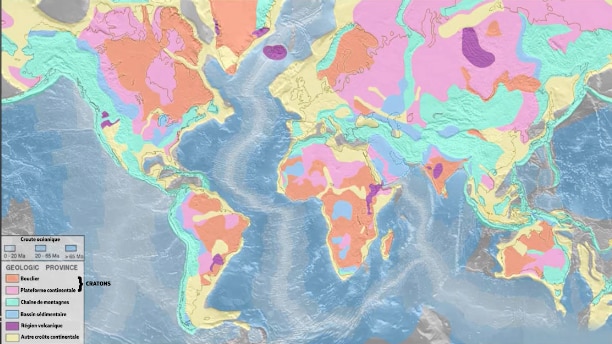
Quand les chercheurs ont mis au point les méthodes de datation radioactive, ils ont cherché les échantillons qu’ils pouvaient utiliser. Les meilleurs échantillons étaient en général des roches magmatiques et, pour palier au fait que les roches continentales sont fortement érodées, ils ont pris des roches dans des cratons (boucliers continentaux). Ce sont des zones de la Terre qui ont été plus stables depuis la formation de la Terre. Les cratons se retrouvent sur cette carte en orangé et en rose.
On en retrouve au niveau de l’Amérique (Nord et Sud) mais aussi en Afrique.
Ce sont des boucliers des zones continentales peu soumises à des transformations. Ce sont des échantillons que l’on a pu soumettre à la méthode de datation radioactive. Les chercheurs ont aussi remarqué qu’en utilisant des échantillons de météorites, on pouvait les dater et approcher aussi la datation de l’âge de la Terre.
Évaluation actuelle de l'âge de la Terre - Partie 2
Évaluation actuelle de l’âge de la Terre – Partie 2
Clair Patterson et l’étude des météorites
Clair Patterson s’est servi d’extrait de météorites retrouvées un peu partout sur Terre. Il a travaillé dans la deuxième moitié du XXe siècle et a donc bénéficié des avancées faites par ses prédécesseurs en termes de datation qui utilisait des éléments radioactifs, notamment des travaux de Rutherford et de la découverte de la radioactivité par Becquerel, à la fin du XIXe siècle.
Clair Patterson a travaillé sur des météorites qui sont des fragments d’astéroïdes. Ce sont des corps trouvés en grande quantité entre Mars et Jupiter. On appelle cela la ceinture d’astéroïdes et ces corps célestes ce sont formés en même temps que le reste du système solaire. En datant les météorites à la surface de la Terre, on date aussi la formation du système solaire et donc l’âge de la Terre. Les météorites ont été des supports de datation plus faciles à utiliser que des roches terrestres. En effet, les météorites se sont peu transformées depuis leur formation, il y a un certain nombre de milliards d’années.
On va voir pourquoi il est plus facile de dater la Terre en fonction des météorites retrouvées plutôt que des roches terrestres car peu de roches terrestres sont utilisables pour la datation.
Différentes météorites étudiées
C. Patterson a travaillé sur différentes météorites : des météorites dont la composition est proche de celle de la Terre globale (chondrites) et des météorites dont la composition est proche d’une enveloppe (manteau : achondrites, noyau : sidérites). Pour rappel, le noyau terrestre est riche en fer principalement, et en nickel.
Il a travaillé sur différents échantillons qui venaient des États-Unis, d’Australie. Il a utilisé un appareil inventé en 1937 pour déterminer la composition des échantillons. Cet appareil est le spectromètre de masse. Il est fondamental dans ces expériences car il a permis de mesurer la composition isotopique des différentes roches. Le spectromètre a permis d’avoir des mesures, puis un certain nombre de calculs pour trouver la composition donnée ici.
Interprétation graphique des rapports isotopiques
A partir de 1955 et sur ces météorites, Patterson s’est intéressé aux isotopes de l’Uranium :
235U radioactif qui se désintègre spontanément en 207Pb
238U radioactif qui se désintègre en 206Pb
On dit que l’Uranium est l’élément père dans les deux cas, et le Plomb l’élément fils ou radiogénique (formé par désintégration radioactive).
Patterson a aussi utilisé une référence stable qui est un isotope du plomb : 204Pb, stable et non radiogénique. Il ne se forme pas par désintégration d’un autre élément et est stable. Donc sa quantité dans une roche, qui est une structure fermée, est donc constante au cours du temps. C’est donc une référence dont la quantité va aussi être évaluée par le spectromètre de masse et qui va servir dans les calculs faits par Patterson.
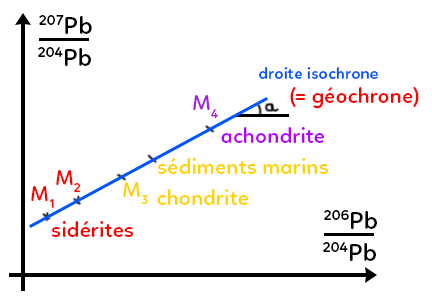
Par des calculs complexes, Patterson a abouti sur une représentation graphique qui est une interprétation graphique des rapports isotopiques. On a le rapport de la quantité de 204Pb sur la quantité de 207Pb dans un échantillon en fonction du rapport entre la quantité de 206Pb sur la quantité de 204Pb.
On construit un graphique qui, pour chaque échantillon, va placer le point qui donne la relation entre ces deux rapports.
Si on travaille sur les météorites étudiées par Patterson, on se rend compte que les sidérites (M1 et M2) sont situées tout en bas du graphique. Les chondrites sont un peu au-dessus (M3), les achondrites proches du manteau se trouvent encore un peu au-dessus (M4) et les sédiments marins ont une composition proche des chondrites (orange).
Si on place tous les échantillons sur lesquels Patterson a travaillé dans ce graphique, on se rend compte qu’ils sont alignés et se placent sur une droite isochrone. Une droite isochrone relie des points qui ont le même temps, c’est-à-dire ici le même âge. Grâce au tracé de cette droite et à l’étude de son coefficient directeur $a,$ on va pouvoir retrouver l’âge de la Terre.
Le coefficient de la droite isochrone est donné par la formule suivante :
$a = C dfrac{e^{lambda_{235U} t}-1}{ e^{lambda_{238U} t}-1}$
$t$ représente l’âge des échantillons. Ces échantillons ont tous le même âge : l’âge de la Terre.
Dans cette formule, pour un élément père donné on a :
$lambda = dfrac{ln2}{T_{1/2}}$
T1/2 étant la demi-vie ou la période.
Dans la formule de $a,$ la seule inconnue est l’âge $t$ : $a$ est mesuré graphiquement, $lambda$ est connu et la constante $C$ vaut $C = (dfrac{^{235}U}{^{238}U})_{act} = dfrac{1}{137,88}$
La résolution de Patterson a abouti à un âge de la Terre égal à 4,55 Ga (+/- 0,07 Ga).
C’est une datation très précise et efficace puisque maintenant, on connaît l’âge de la Terre avec précision et la Terre a 4,567 Ga. Notre planète a environ 4,6 Ma et Patterson, au milieu du XXe siècle, avait relativement bien évalué cette âge grâce aux isotopes radioactifs des météorites.
Dernière chose, la droite isochrone pour les roches de la Terre peut être appelée géochrone. Patterson l’a appelée ainsi puisqu’il ne s’agit pas de n’importe quel isochrone de n’importe quelle planète : il s’agit ici de donner l’âge de notre planète Terre.