La musique ou l'art de faire entendre les nombres
La musique ou l’art de faire entendre les nombres
Pour faire de la musique, il faut qu’elle soit agréable à l’oreille et cela est régi par des règles mathématiques. On présente ainsi l’aspect mathématique de la musique : les rapports de fréquence qu’on peut faire entre les notes et pourquoi ces rapports sont-ils si importants.
I. La musique s’adapte à l’oreille humaine
L’oreille humaine est sensible aux rapports de fréquence entre deux sons. Les rapports de fréquences seront définis comme des intervalles. L’intervalle $J$ c’est : $J = dfrac{f_1}{f_2}$. Ces deux notes de fréquences $f_1$ et $f_2$ sont consonantes si l’intervalle $J$ est une fraction entière (c’est-à-dire un nombre entier divisé par un autre nombre entier).
Dans les autres cas, on dit que les deux notes sont dissonantes. Deux des intervalles consonants les plus important dont on va parler ici sont :
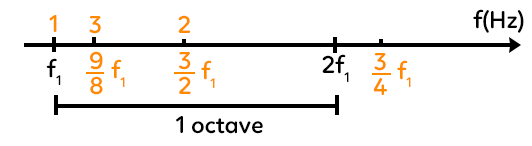
– l’octave : intervalle de 2 entre deux notes $J = dfrac{2}{1}$. Par exemple, une première note a une fréquence de 100 Hz, la seconde a une fréquence de 200 Hz s’il y a une octave.
– la quinte : intervalle de $dfrac{3}{2}$ entre deux notes $J=dfrac{3}{2}$. Par exemple, si on prend une note à la fréquence de 100 Hz, la deuxième est à la fréquence de 150 Hz.
II. Construire une gamme
A. Gamme
Une gamme est une suite finie de notes réparties sur une octave. On va choisir une série de notes ayant des fréquences comprises entre $f_1$ et $2f_1$.
B. Gamme de Pythagore en 12 notes
On s’intéresse à la gamme de Pythagore. Il y a 12 notes sur cette octave comprises entre $f_1$ et $2f_1$.
Pythagore a choisi que toutes les notes qu’il crée soient dans un rapport consonant entre elles. Pour faire cela, on part de la fréquence $f_1$ et on construit la note $f_2$ en prenant la quinte de la première note. Cela revient à faire $dfrac{3}{2}f_1$. Ensuite, on prend la quinte de la deuxième note. On a alors $dfrac{9}{4}f_1$. La troisième note sort de l’intervalle car on est au-delà de l’octave.
Pythagore divise la fréquence par deux lorsqu’elle sort de l’octave. On a alors $dfrac{9}{8}f_1$ qui va revenir dans l’intervalle. Et ainsi de suite pour les autres notes.
À chaque fois, on a des rapports qui sont des fractions entières donc toutes les notes sont consonantes les unes avec les autres.
C. Gamme complète
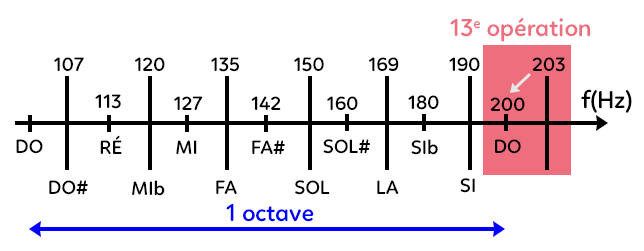
Voici la gamme complète de Pythagore en 12 notes.
On a choisi pour des questions de facilité $f_1 = 100 Hz$. On a d’abord le DO à 100 Hz, puis à 107 Hz le DO#, etc. On a construit 12 notes et ce qui est intéressant mais problématique dans la gamme de Pythagore c’est la 13e note. Pythagore voulait que lorsque la gamme est finie, la 13e note tombe exactement sur l’octave. Or, ce n’est pas le cas. La 12e note créée est le FA et lorsqu’on crée la 13e note à partir du FA, on tombe sur une note de fréquence 203 Hz. C’est proche de 200 Hz donc on va forcer cette dernière note à tomber pile sur l’octave.
Or, si on essaye de créer un accord entre le FA et le DO créé, on va avoir quelque chose de dissonant. En effet, on aura plus de fraction entière et donc de consonance. On s’arrange pour créer les partitions sans ces accords-là. Le problème c’est que si on fait cela, la partition ne peut pas être changée de tonalité. Si on change de tonalité, on risque de jouer cet accord-là et cela ne va pas marcher puisque cela va être désagréable à l’oreille. Pour résoudre ce problème, une gamme tempérée a été créée.
Construction de la gamme tempérée
Construction de la gamme tempérée
Il est conseillé de prendre d’abord connaissance du cours « la musique ou l’art de faire entendre les nombres » car il explique comment se construit une gamme pythagoricienne.
I. Le problème de la gamme pythagoricienne
Sa note finale est dissonante. Il est donc impossible de changer la tonalité d’un morceau musical. Pour remédier à ce problème, on a proposé de construire une autre gamme d’une autre manière qui s’appelle : la gamme tempérée à 12 notes.
II. La gamme tempérée à 12 notes
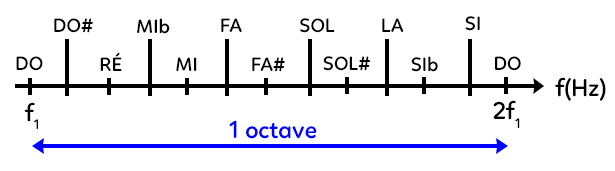
Comment construit-on cette gamme ? C’est assez simple : on a une première note DO à une fréquence $f_1$ et on va jusqu’à l’octave suivant de fréquence $2f_1$ qui est aussi un DO.
Entre ces deux DO, on a une succession de 12 notes. L’idée générale de la construction de la gamme est de prendre des intervalles réguliers entre chacune des notes. Donc l’intervalle de fréquence entre le DO et le RE doit être le même qu’entre le RE et le MI, par exemple.
Pour construire les notes, on utilise : $f_2 = Jf_1$, $f_3 = Jf_2 = Jtimes Jtimes f_1$.
Si bien que lorsqu’on veut obtenir la dernière note, on a : $f_13 = Jtimes J times … times J times f_1 = 2f_1$.
$J$ est multiplié 12 fois. On veut retomber exactement pile sur l’octave donc on veut que $f_13 = 2f_1$.
Que vaut $J$ ?
$J$ multiplié 12 fois vaut 2 (en simplifiant les $f_1$ de la formule précédente). On a alors $J^{12}= 2$.
On peut prendre un cas plus simple : $J^2 = 2$. On voudrait la valeur de $J.$ On obtient alors : $J = sqrt{2} = 2^{frac{1}{2}}$.
On omet le cas négatif. On voit alors que $J^{12} = 2^{frac{1}{12}}= 1,05946…$.
L’intervalle définit ici est un irrationnel. Les irrationnels sont des nombres qui peuvent se définir comme la fraction de deux entiers. On a appelé cela les intervalles consonants. Si $J$ est un irrationnel, l’intervalle entre chacune des notes définies par la gamme tempérée est dissonant. Aucun intervalle n’est consonant. C’est très loin de l’idéal pythagoricien !
Ce qui est intéressant dans la gamme tempérée c’est qu’à la fin de la 12e note on retombe exactement sur l’octave. Cela permet de changer la tonalité d’un morceau musical sans avoir la très forte dissonance de la dernière note sur la gamme pythagoricienne. On construit les partitions actuelles sur ces gammes tempérées.