Repérage sur une droite graduée
Repérage sur une droite graduée
Pour placer une fraction sur une droite graduée, on commence par lire le dénominateur.
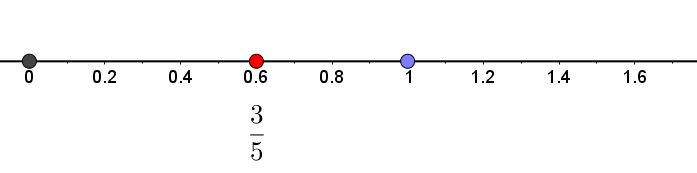
Exemple : $\dfrac{3}{5}$.
Ici, le dénominateur est $5$, cela signifie que l’on va partager l’unité de l’axe gradué en cinq parties égales.
Chaque partie représente un cinquième de l’unité.
Ensuite, on regarde le numérateur de la fraction.
Si on reprend l’exemple précédent, on part de l’origine puis on se déplace dans le sens croissant en comptant $3$ espaces.
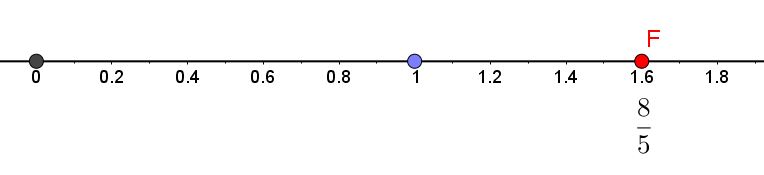
On souhaite désormais placer $\dfrac{8}{5}$.
On commence donc par diviser chaque grand espace en cinq parties égales.
En partant de l’origine, il faut se déplacer de 8 espaces.
On remarque alors que $\dfrac{8}{5} > 1$. En outre, en partant de $1$, on se déplace de $\dfrac{3}{5}$ pour atteindre $\dfrac{8}{5}$.
Ainsi, on vient de montrer que
$\dfrac{8}{5} = 1 + \dfrac{3}{5}$.
En partant de $2$, on remarque que l’on se déplace de 2 espaces vers la gauche. Ainsi,
$\dfrac{8}{5} = 2 – \dfrac{2}{5}$
A l’inverse, il est possible que le but d’un exercice soit de déterminer la valeur d’un point, préalablement placé sur un axe gradué, que l’on appelle aussi l’abscisse d’un point.
Autres exemples
a)
On remarque que la graduation indiquée est de $0.1=\dfrac{1}{10}$.
Pour trouver le nombre associé à $C$, il faut compter le nombre de petites graduations comprises entre l’origine et $\dfrac{1}{10}$.
On trouve dix petites graduations. On partage ainsi un dixième en dix parties égales, ce qui signifie qu’une partie vaut un centième.
Donc, une petite graduation vaut $\dfrac{1}{100}$.
Ensuite, il s’agit de compter le nombre d’espaces entre l’origine et le point $C$.
On trouve alors $\dfrac{7}{100}$.
Ainsi, l’abscisse de $C$ est $\dfrac{7}{100}$.
b)
L’abscisse du point $D$ est $\dfrac{1}{10} + \dfrac{6}{100}$.
Pour écrire ce nombre en une seule fraction, il faut se souvenir des fractions décimales.
$\dfrac{1}{10} + \dfrac{6}{100} = 0,1 + 0,06 = 0,16 = \dfrac{16}{100}$.