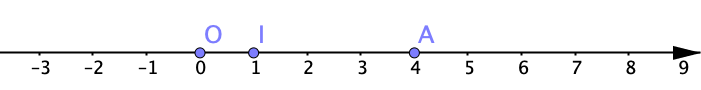Intersections et réunions d'intervalles - exemples
Intersections et réunions d’intervalles – exemples
Définitions
1) L’intersection de deux intervalles $I$ et $J$ contient tous les éléments qui appartiennent à la fois à $I$ et à la fois à $J$.
Elle est notée $I \cap J$ et se lit $I$ inter $J$.
2) La réunion de deux intervalles $I$ et $J$ contient tous les éléments qui appartiennent à $I$ ou bien à $J$ ou bien à la fois à $I$ et à la fois à $J$.
Elle est notée $I \cup J$ et se lit $I$ union $J$. .
Méthode :
Considérons les deux intervalles suivants $I = [-5, 4]$ et $J = ]- \infty, 2]$ que l’on peut représenter sur un graphique.

La représentation graphique permet de visualiser les notions d’intersection et de réunion.
Ainsi l’intersection correspond aux abscisses où les deux zones hachurées sont représentées : $I \cap J = [-5, 2]$.
Enfin, la réunion correspond aux abscisses où au moins une zone hachurée est représentée : $I \cup J = ]- \infty, 4]$.
Ensemble R - Intervalles
Ensemble des nombres réels $\mathbb{R}$ – Intervalles
Définition
L’ensemble des nombres utilisés au quotidien (les nombres négatifs, positifs, décimaux, …) est appelé l’ensemble des réels, et est noté $\mathbb{R}$.
On peut représenter l’ensemble de ces nombres réels par une droite gradué, munie d’une origine $O$, d’une unité et orientée vers les nombres positifs.
On a placé sur la droite le point $A$ qui correspond au nombre $4$. On dit que $A$ a pour abscisse $4$.
Ainsi, à chaque nombre réel correspond un point sur la droite et réciproquement.
On peut indiquer sur la droite le symbole $+ \infty$, qui est le symbole de l’infini pour signifier que la droite ne s’arrête pas.
Intervalles dans $\mathbb{R}$
On s’intéresse désormais à une partie de la droite, comprise entre $I$ et $A$.
L’ensemble de ces réels compris entre les abscisses des points $I$ et $A$ est appelé un intervalle.
La notation de l’intervalle est la même que pour un segment.
Par exemple, l’intervalle entre les abscisses des points $I$ et $A$ se note $[1; 4]$.
Si l’abscisse du point $I$ n’appartient par à l’intervalle, on utilisera un crochet ouvert pour le signifier.
On notera alors $]1; 4]$.
Il existe différents types d’intervalles.
| Intervalle | Inégalité | Droite |
| $[a; b]$ | $a \leq x \leq b$ | |
| $]a; b]$ | $a < x \leq b$ | |
| $[a; + \infty [$ | $a \leq x$ | |
| $]- \infty; a [$ | $x < a$ |
Pour simplifier l’écriture de certains intervalles, on utilise des notations particulières.
Ainsi, $\mathbb{R}^+$ correspond à l’ensemble des nombres réels positifs, que l’on peut aussi noter $[0; +\infty [$.
$\mathbb{R}^-$ correspond à l’ensemble des nombres réels négatifs, que l’on peut aussi noter $]- \infty; 0]$.
Enfin, $\mathbb{R}^*$ correspond à l’ensemble des nombres réels privés de 0, que l’on note aussi $\mathbb{R} \backslash 0$.
Intersection de deux intervalles $I$ et $J$
L’intersection des intervalles $I$ et $J$ est composé de tous les éléments communs à $I$ et à $J$ en même temps.
On note l’intersection par $I \cap J$ et cela se lit $I$ inter $J$.
Exemples :
1) Déterminons $[-1; 2[ \cap [0; 3]$.
Pour cela, on peut sur la droite graduée hachurer le premier intervalle puis le second intervalle. L’intersection correspond à l’intervalle hachuré deux fois.
On trouve alors $[-1; 2[ \cap [0; 3] = [0; 2[$
2) Déterminons $[1;2] \cap [3; + \infty [$.
On remarque que $2 < 3$, donc aucun élément n’est commun aux deux intervalles.
On dira que l’intersection est égale à l’ensemble vide et se note $ \varnothing$.
Ainsi : $[1;2] \cap [3; + \infty [=\varnothing$
Réunion de deux intervalles $I$ et $J$
La réunion des intervalles $I$ et $J$ est composée de tous les éléments appartenant à $I$ ou à $J$.
La réunion peut aussi contenir des éléments appartenant à la fois à $I$ et à $J$.
La réunion se note $I \cup J$ et se lit $I$ union $J$.
Exemples
1) Déterminons $[-1; 2[ \cup [0; 3]$.
Pour cela, on peut sur la droite graduée hachurer les deux intervalles. La réunion correspond à l’intervalle hachuré au moins une fois.
On trouve alors $[-1; 2[ \cup [0; 3] = [-1; 3]$
2) Déterminons $[1;2] \cup [3; + \infty [$.
On remarque qu’il n’y a pas de simplification possible de l’écriture.
On écrit donc la réunion sous la forme $[1;2] \cup [3; + \infty [$.