Déterminant de deux vecteurs, critère de colinéarité
Ce cours du chapitre Vecteurs, coordonnées aborde le déterminant de deux vecteurs et le critère de colinéarité. D’abord, il se concentre sur le déterminant de deux vecteurs dans une base orthonormée (définition, exemple). Puis, il donne la définition de deux vecteurs colinéaires, le critère de colinéarité et fait une démonstration.
Déterminant de deux vecteurs, critère de colinéarité : ce que tu vas réviser
I. Déterminant de deux vecteurs dans une base orthonormée
Comment calculer le déterminant de deux vecteurs ?
A. Définition d’un déterminant à deux vecteurs
Soit $(\overrightarrow{i}, \overrightarrow{j})$ une base orthonormée.
Soient $\overrightarrow{u} \left ( \begin{array}{c} x_1 \\ y_1 \end{array} \right )$ et $\overrightarrow{v} \left ( \begin{array}{c} x_2 \\ y_2 \end{array} \right )$ deux vecteurs exprimés dans cette base.
On appelle déterminant des deux vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$ le réel $x_1y_2 – y_1x_2$.
On note :
$Det(\overrightarrow{u}, \overrightarrow{v}) = \left | \begin{array}{cc} x_1 & x_2 \\ y_1 & y_2 \end{array} \right | = x_1y_2 – y_1x_2$
B. Exemples de déterminant à deux vecteurs
$Det(\overrightarrow{i}, \overrightarrow{i}) = \left | \begin{array}{cc} 1 & 1 \\ 0 & 0 \end{array} \right | = 1 \times 0 – 0 \times 1 = 0$
$Det(\overrightarrow{i}, \overrightarrow{j}) = \left | \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right | = 1 \times 1 – 0 \times 0 = 1$
II. Colinéarité de deux vecteurs
A. Définition de deux vecteurs colinéaires
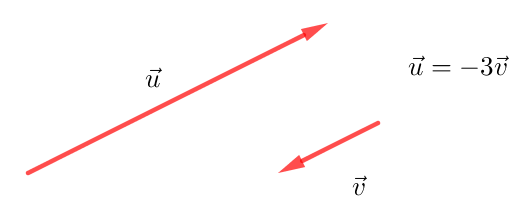
Deux vecteurs non nuls $\overrightarrow{u}$ et $\overrightarrow{v}$ sont colinéaires signifie qu’il existe un réel $k$ tel que
$\overrightarrow{u} = k\overrightarrow{v}$.
Si $k>0$, les vecteurs ont le même sens, si $k<0$ les vecteurs sont de sens opposé.
Exemple avec $k=-3$
Remarque : le vecteur nul $\overrightarrow{0}$ est colinéaire à tout vecteur.
B. Le critère de colinéarité
Comment savoir si deux vecteurs sont colinéaires ?
Pour savoir si deux vecteurs sont colinéaires, on utilise le critère de colinéarité.
Soit $(\overrightarrow{i}, \overrightarrow{j})$ une base orthonormée.
Soient $\overrightarrow{u} \left ( \begin{array}{c} x_1 \\ y_1 \end{array} \right )$ et $\overrightarrow{v} \left ( \begin{array}{c} x_2 \\ y_2 \end{array} \right )$ deux vecteurs exprimés dans cette base.
$\overrightarrow{u}$ et $\overrightarrow{v}$ sont colinéaires si et seulement si $det(\overrightarrow{u}, \overrightarrow{v}) = 0$,
ou encore si et seulement si $x_1y_2 – y_1x_2 = 0$.
C. Démonstration du critère de colinéarité
Pour démontrer ce critère, on raisonne par disjonction de cas. En séparant tous ces cas puis en les étudiant chacun séparément, on aura après réunion de chacun des cas ainsi étudiés tous les cas possibles.
Le premier cas correspond au cas où un des vecteurs est nul.
Le deuxième cas correspond au cas où les deux vecteurs ne sont pas nuls.
a) Premier cas : on suppose qu’un des vecteurs est nul
On suppose arbitrairement que $\overrightarrow{u} = \overrightarrow{0}$.
On démontre le sens direct de la condition nécessaire et suffisante puis la réciproque.
On suppose donc dans un premier temps que $\overrightarrow{u}$ et $\overrightarrow{v}$ sont colinéaires.
On calcule alors $det(\overrightarrow{u}, \overrightarrow{v}) = x_1y_2 – y_1x_2 =0 \times y_2 – 0 \times x_2 = 0$.
On suppose désormais que $x_1y_2 – y_1x_2 = 0$.
Or on sait que le vecteur nul est colinéaire à tout vecteur, en particulier, il est colinéaire au vecteur $\overrightarrow{v}$.
b) Deuxième cas : on suppose que les deux vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$ sont non nuls.
On suppose dans un premier temps que $\overrightarrow{u}$ et $\overrightarrow{v}$ sont colinéaires. Il existe donc un réel $k$ tel que $\overrightarrow{u} = k\overrightarrow{v}$, c’est-à-dire que $\left \{ \begin{array}{c} x_1 = kx_2 \\ y_1 = ky_2 \end{array} \right.$
On calcule alors $det(\overrightarrow{u}, \overrightarrow{v}) = x_1y_2 – y_1x_2 = kx_2y_2 – ky_2x_2 = 0$.
On suppose que $x_1y_2 – y_1x_2 = 0$ donc $x_1y_2 = y_1x_2$.
On doit alors distinguer deux cas.
1 – Soit $y_2 \neq 0$
On peut alors diviser par $y_2$. Ainsi, $x_1 = \dfrac{y_1}{y_2}x_2$.
En posant $k = \dfrac{y_1}{y_2}$, on a alors $\left \{ \begin{array}{l} x_1 = kx_2 \\ y_1 = y_1 \times \dfrac{y_2}{y_2} = \dfrac{y_1}{y_2} \times y_2 = k y_2 \end{array} \right.$.
2 – Soit $y_2 = 0$
On a alors $0 = y_1x_2$, or un produit est nul si et seulement si un de ces facteurs est nul ce qui signifie que $y_1 = 0$ ou $x_2 = 0$.
Si $x_2 = 0$ alors comme $y_2 = 0$, cela impliquerait que $\overrightarrow{u} = \overrightarrow{0}$ ce qui n’est pas possible d’après l’hypothèse du cas 2. Donc, on en déduit que $y_1 = 0$.
On peut alors réécrire les vecteurs : $\overrightarrow{u} \left ( \begin{array}{c} x_1 \\ 0 \end{array} \right )$ et $\overrightarrow{v} \left ( \begin{array}{c} x_2 \\ 0 \end{array} \right )$.
Ces deux vecteurs ont des directions parallèles à l’axe des abscisses et on peut écrire $\overrightarrow{u} = k\overrightarrow{v}$, avec $k = \dfrac{x_1}{x_2}$.
Pour aller plus loin dans Vecteurs, coordonnées
Après avoir étudié ce cours, nous te conseillons de poursuivre avec ces autres notions :


