Définition vectorielle des homothéties

Définition vectorielle des homothéties

Définition vectorielle des homothéties

I) Définition

Soient $O$ un point du plan et $k$ un réel non nul. 

On appelle homothétie de centre $O$ et de rapport $k$ la transformation qui à tout point $M$ associe le point $M’$ tel que $\overrightarrow{OM’} = k \overrightarrow{OM}$. 

Si on note $h$ l’homothétie de centre $O$ et de rapport $k$, les énoncés suivants sont équivalents. 

$M’$ est l’image de $M$ par $h$ 

$M’ = h(M)$

$\overrightarrow{OM’} = k \overrightarrow{OM}$

Exemples : 

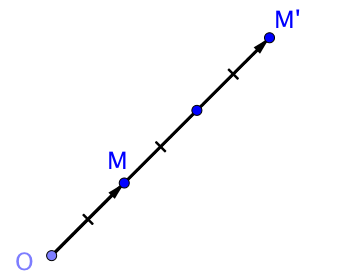
Dans cette figure, on a divisé le segment $[OM’]$ en trois segments de même longueur égale à celle du segment $[OM]$. 

Ainsi, on a $\overrightarrow{OM’} = 3 \overrightarrow{OM}$. C’est donc une homothétie de centre $O$ et de rapport $3$.

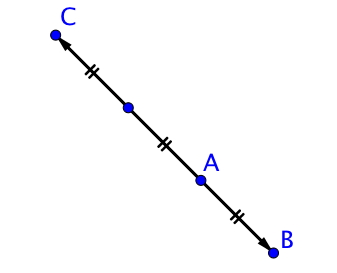
Sur le schéma ci-dessus, on peut écrire l’égalité vectorielle suivante :

$\overrightarrow{AC} = -2 \overrightarrow{AB}$.

Il s’agit donc d’une homothétie de centre $A$ et de rapport $-2$ : le point $C$ est l’image du point $B$ par l’homothétie de centre $A$ et de rapport $-2$.

Conséquences : 

Les points $O, M, M’$ sont alignés, car les vecteurs $\overrightarrow{OM’}$ et $\overrightarrow{OM}$ sont colinéaires. 

$O$ est sa propre image, on dira alors que $O$ est invariant par l’homothétie de centre $O$. 

Si $A, B, C$ sont trois points alignés, avec $A$ distinct de $B$ et de $C$, alors il existe une unique homothétie de centre $A$ qui transforme $B$ en $C$. 

Une symétrie centrale est une homothétie de centre $O$ et de rapport $(-1)$. 

II) Propriétés 

a) Propriété fondamentale 

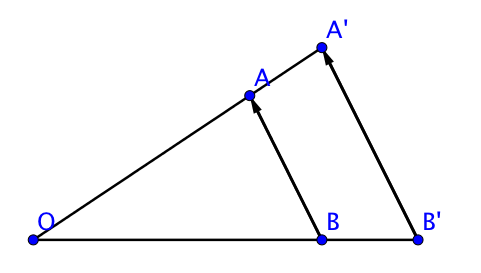
On considère une homothétie $h$ de centre $O$ et de rapport $k$.

Soient $A$ et $B$ deux points. 

Si $A’ = h(A)$ et $B’ = h(B)$, alors $\overrightarrow{A’B’} = k \overrightarrow{AB}$.

Preuve : 

$A’ = h(A)$ signifie que $\overrightarrow{OA’} = k \overrightarrow{OA}$.

$B’ = h(B)$ signifie que $\overrightarrow{OB’} = k \overrightarrow{OB}$.

En outre, $\overrightarrow{A’B’} = \overrightarrow{A’O} + \overrightarrow{OB’} = – k \overrightarrow{OA} + k \overrightarrow{OB} =  k (\overrightarrow{AO} + \overrightarrow{OB} = k \overrightarrow{AB}$

b) Image d’une droite 

Propriété :

Une homothétie transforme une droite $(d)$ en une droite $(d’)$ parallèle à $(d)$. 

Si $(d)$ passe par le centre de l’homothétie, alors $(d’)$ et $(d)$ sont confondues. 

c) Théorème de Thalès 

 .   

Théorème : 

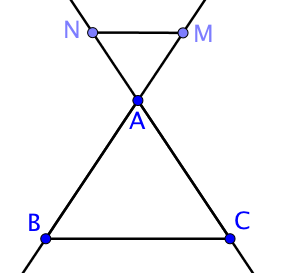
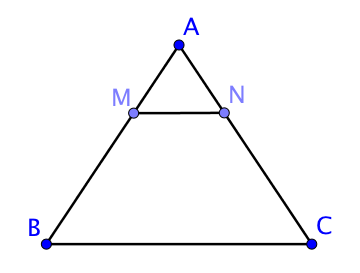
Soit $ABC$ un triangle, $M \in (AB)$ et $N \in (AC)$.

Si $(MN) // (BC)$ alors l’homothétie de centre $A$ qui transforme $B$ en $M$ transforme aussi $C$ en $N$. 

III) Effet des homothéties

Les distances sont multipliées par $|k|$. 

Les surfaces sont multipliées par $k^2$.

Les volumes sont multipliée par $|k|^3$.

L’homothétie conserve l’alignement : l’image de trois points alignés par une homothétie est trois points points alignés. 

L’homothétie conserve le parallélisme : si deux droites sont parallèles, leurs images seront aussi deux droites parallèles.