Le cercle
Le cercle
Définition
Un cercle est formé de tous les points situés à la même distance d’un point appelé « centre ».
Cette distance commune est appelée « rayon ».
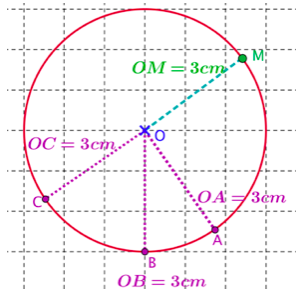
Si $\mathcal{C}$ est le cercle de centre $O$ et de rayon $r$, l’écriture « $M \in \mathcal{C}$ » signifie que la distance $OM$ est égale à $r$
Exemple :
si $\mathcal{C}$ est le cercle de centre $O$ et de rayon $3$cm, $M \in \mathcal{C}$ signifie que $OM=3$cm
Vocabulaire
Soit $\mathcal{C}$ le cercle de centre $O$ et de rayon $r$, où $r$ est un nombre positif donné.
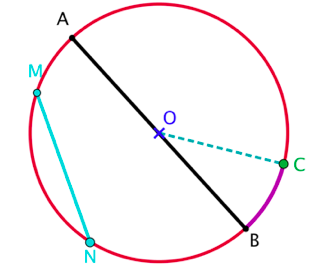
Si $C$ est un point du cercle $\mathcal{C}$ on dit que le segment $[OC]$ est un rayon du cercle.
Si $M$ et $N$ sont deux points du cercle $\mathcal{C}$ on dit que le segment $[MN]$ est une corde du cercle.
Une corde passant par le centre du cercle est appelée diamètre du cercle $\mathcal{C}$. Par exemple, le segment $[AB]$ est un diamètre du cercle.
La portion du cercle comprise entre les points $B$ et $C$ est un arc de cercle.
Le petit plus des bons profs
Deux formules supplémentaires sur le cercle à retenir:
Etant donné un cercle de rayon $R$
- Le périmètre du cercle est égal à : $P= 2\pi R$
- L’ aire du disque est égale à : $A=\pi R^2$