Unités de longueurs, masses, durées
Unités de longueurs, masses, durées
Unités de longueurs usuelles
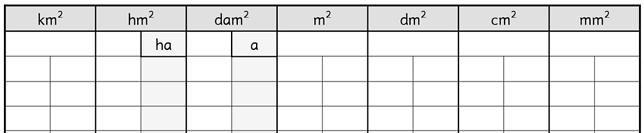
Pour convertir des unités de longueurs, on utilise le tableau suivant :
| $km$ | $hm$ | $dam$ | $m$ | $dm$ | $cm$ | $mm$ |
| 1 | ||||||
| 1 |
Unités de masses usuelles
Pour convertir des unités de masses, on utilise le tableau suivant :
| $kg$ | $hg$ | $dag$ | $g$ | $dg$ | $cg$ | $mg$ |
| 1 | ||||||
| 1 |
1 tonne = 1000kg
Unités de durées usuelles
A connaître par cœur :
- 1 année = 1 an = 12 mois = 365 jours ;
- 1 jour = 24 heures
- 1 heure = 60 minutes = 60 x 60 = 3 600 secondes ;
- 1 minute = 60 secondes
Conversions heures, minutes, secondes
Attention 1,5h est différente de 1h50 min. En effet :
$1,5h = 1h+0,5 h$
$1,5h = 1h + 0,5\times 60$ min
$1,5h = 1h + 30$ min. On le savait déjà ! Une heure et demi correspond à une heure et trente minutes.
Commentaire
On utilise les unités de durées tous les jours dans sa vie d’élève ou d’adulte. Tu peux les rencontrer pour les temps de transport mais aussi des calculs de vitesse. Attention aux conversions : les unités de durées (heures, minutes) ne sont pas en base 100.
Le saviez-vous ?
Que représente une année lumière ? Un temps, une distance ?
Attention, il s’agit d’une distance : celle que la lumière parcourt en une année. La lumière se déplace à la vitesse vertigineuse de 300 000 km par seconde (7 fois le tour de la terre en une seconde). Pour information, la lumière parcourt aussi la distance terre-lune en une seconde.
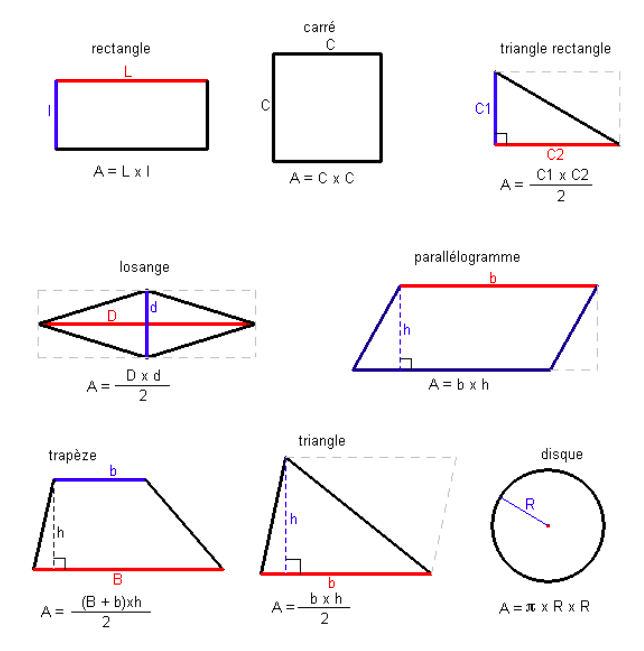
Aires de figures usuelles
Aires de figures usuelles
Définition
L’aire d’une figure est la mesure de la partie qui se trouve à l’intérieur de la figure
Il faut connaître en priorité les formules de l’aire du triangle, du rectangle et du disque : beaucoup d’exercices portent sur ces figures.
Unités d’aires
L’unité principale de mesure de l’aire est le $m^2$. On utilise ce type de tableau pour convertir les aires :
- Are : $1a=100m^2$
- Hectare : $1ha = 100a = 10\ 000m^2$
Exemple :
L’aire d’un carré de côté $15$ m vaut :
$A = 15^2 = 225m^2$.
Cette aire vaut aussi $2,25 dam^2$ ou encore : $22 500 dm^2$
Commentaire :
C’est un grand classique. On change d’une unité d’aire en multipliant ou divisant par 100.
Volumes de pavés et changement d’unités
Volumes de pavés, changement d’unités
Volume d’un parallélépipède rectangle ou Pavé droit
Le volume d’un solide est la partie remplissant l’intérieur du solide. L’unité principale de mesure du volume est le $m^3$.
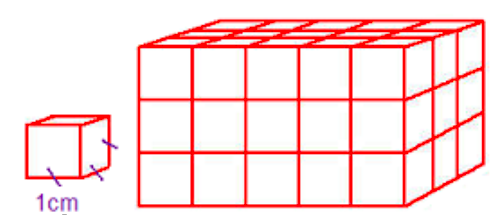
On utilise aussi d’autres unités : dans cet exemple, le volume du pavé est :
$V=5\times 3\times 3 = 45 cm^3$ (Le petit cube rouge a un volume de $1cm^3$ et le pavé est composé de $45$ petits cubes identiques)
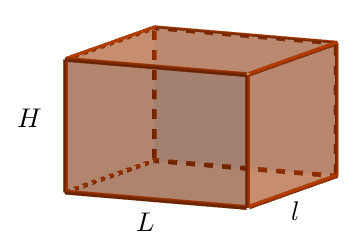
Formule du volume d’un pavé droit
$V=l\times L\times H$
à retenir : $V= Longueur\times largeur\times hauteur$
Exemple :
Dans la figure ci-contre, on choisit :
$L=3m, l=1,5m$ et $H = 1,2m$
On a : $V = 3\times 1,5\times 1,2$
$V = 5,4 m^3$
Unités de volumes
Pour calculer le volume, on multiplie 3 grandeurs : la longueur, la largeur et la hauteur.
C’est pour cela que l’unité de volume est le $m^3$ (on dit “mètre cube”).
Pour mesurer les capacités, on utilise : Le litre et ses unités associées.
À retenir : $1 L= 1 dm^3$