Agrandissement - Réduction

Agrandissement – Réduction

Propriétés

Lorsque l’on réalise un agrandissement ou une réduction d’une figure ou d’un solide, toutes les longueurs sont multipliées par un coefficient multiplicateur $k$.

Les aires sont multipliées par $k^2$ et les volumes sont multipliés par $k^3$. 

Lorsqu’il s’agit d’un agrandissement, le coefficient $k$ est supérieur strictement à 1.

Lorsqu’il s’agit d’une réduction, le coefficient $k$ est inférieur strictement à 1 et positif.

1)

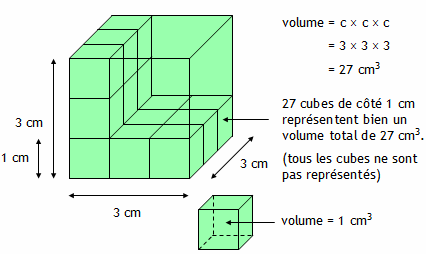
Par exemple, le cube a été agrandit d’un coefficient égal à 3. Ses surfaces ont donc été multipliées par 9.

Le cube ainsi agrandi est donc 27 fois plus volumineux que le cube initial. 

2)

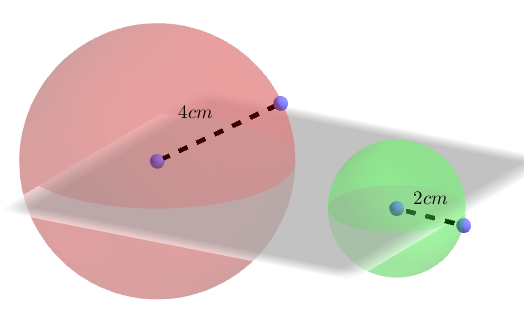
Le rayon de la boule a été réduit de moitié. Le coefficient multiplicateur est donc égal à 0,5 : le diamètre est deux fois plus petit.

La surface de la sphère est donc multipliée par $(0,5)^2=0,25$

Le volume de la boule est multiplié par $(0,5)^3=0,125$.