Angles inscrits, angles au centre

Angles inscrits - Angles au centre

Angles inscrits – Angles au centre

Définition 

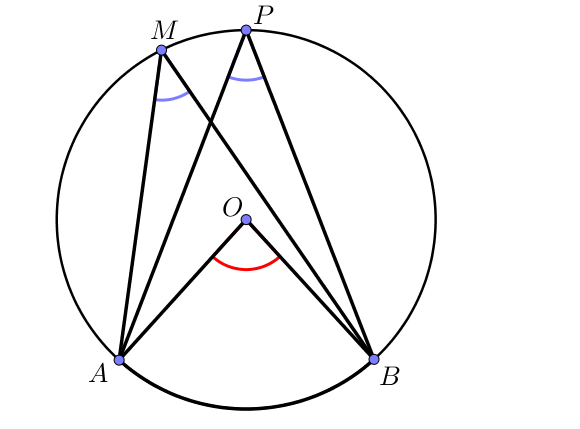
Un angle inscrit est un angle dans un cercle dont le sommet appartient au cercle et dont les côtés coupent le cercle en formant un arc de cercle appelé arc intercepté.

Un angle au centre est un angle dont le sommet est le centre du cercle et dont les côtés coupent le cercle.

Théorèmes

Dans un cercle, deux angles inscrits qui interceptent le même arc sont égaux.  

Dans un cercle, l’angle inscrit mesure la moitié de l’angle au centre associé (qui intercepte le même arc). 

Exemple :

Supposons par exemple que $\widehat{AMB} = 20°$.

Il s’agit d’un angle inscrit interceptant l’arc $\overset{\frown}{AB}$. 

L’angle $\widehat{APB}$ est aussi un angle inscrit qui intercepte le même arc, ainsi $\widehat{APB} = 20°$.

Enfin, l’angle $\widehat{AOB}$ est un angle au centre associé aux deux angles inscrits précédents, ainsi, $\widehat{AOB} = 40°$.