Exponentielle - Croissances comparées
Croissances comparées
Pour $n$ appartenant à $\mathbb{N}$ :
1. $\displaystyle \lim \limits_{x \rightarrow +\infty} \frac{e^x}{x} = +\infty$ ; $\displaystyle \lim \limits_{x \rightarrow +\infty} \frac{e^x}{x^n}=+\infty$
2. $\displaystyle \lim \limits_{x \rightarrow -\infty} xe^x =0$ ; $\displaystyle \lim \limits_{x \rightarrow -\infty} x^ne^x =0$
A savoir aussi :
3. $ \displaystyle\lim_{x\to 0} \frac {e^x-1}{x}=1$
Exercice 1
Calculer : $\displaystyle \lim \limits_{x \rightarrow +\infty} x^3 -e^x$.
Corrigé
- étape 1 : On s’interroge sur la présence de formes indéterminées.
Il y en a une de la forme $\infty-\infty$. - étape 2 : On factorise par $e^x$ le numérateur et le dénominateur.
$\displaystyle \lim \limits_{x \rightarrow +\infty} e^x(\frac{x^3}{e^x}-1)$ - étape 3 : On utilise le théorème des croissances comparées.
On sait que $\displaystyle \lim \limits_{x \rightarrow +\infty} \frac{e^x}{x^3} = +\infty$.
Donc $\displaystyle \lim \limits_{x \rightarrow +\infty} \frac{x^3}{e^x} =\displaystyle \lim \limits_{x \rightarrow +\infty} \frac{1}{\frac{e^x}{x^3}}= 0$.
Le terme entre parenthèses tend donc vers $-1$.
- étape 4 : Par produit de limites, on conclut donc :
$\displaystyle \lim \limits_{x \rightarrow +\infty} x^3 -e^x= -\infty$
Exercice 2
Calculer : $\displaystyle \lim \limits_{x \rightarrow +\infty} \frac{e^x-x}{2e^x+3}$.
Corrigé
- étape 1 : On s’interroge sur la présence de formes indéterminées.
Il y en a au moins une au numérateur (de la forme $\infty-\infty$).
- étape 2 : On factorise par $e^x$ le numérateur et le dénominateur.
$\displaystyle\lim \limits_{x \rightarrow +\infty} \frac{e^x-x}{2e^x+3}=\displaystyle \lim \limits_{x \rightarrow +\infty} \frac{e^x(1-\frac{x}{e^x})}{e^x(2+\frac{3}{e^x})} = \displaystyle \lim \limits_{x \rightarrow +\infty} \frac{1-\frac{x}{e^x}}{2+\frac{3}{e^x}}$
- étape 3 : On utilise le théorème des croissances comparées.
$\displaystyle \lim \limits_{x \rightarrow +\infty} \frac{x}{e^x} = 0$ et $\displaystyle \lim \limits_{x \rightarrow +\infty} \frac{3}{e^x}=0 $
- étape 4 : le numérateur tend vers $1$ et le dénominateur tend vers $2$. On conclut donc :
$\displaystyle \lim \limits_{x \rightarrow +\infty} \frac{e^x-x}{2e^x+3}= \frac{1}{2}$
Fonctions composées - exp(u(x)) - Exercice
Exercice
Étudions la fonction \(f(x) = \large\frac{3e^x}{e^{2x} + 1}\).
Étape 1 : On cherche toujours l’ensemble de définition d’une fonction.
Étape 2 : On cherche les limites aux bornes de l’intervalle : en \(+\infty\) et en \(-\infty\).
Étape 3 : On factorise pour lever l’indétermination.
Étape 4 : On utilise ici que \(\displaystyle\lim_{x \to -\infty} e^x = 0\).
Étape 5 : On utilise la formule \((\frac{u}{v})’ =\large \frac{u’v – uv’}{v^2}\) pour étudier les variations.
Théorème des valeurs intermédiaires
Théorème des valeurs intermédiaires
Théorème
Soient $f$ une fonction continue sur un intervalle $I$ et $a$ et $b$ deux réels dans l’intervalle $I$ tels que $a\leqslant b $.
Alors, pour tout réel $k$ compris entre $f(a)$ et $f(b)$, il existe au moins un réel $c$ compris entre $a$ et $b$ tel que $f(c)=k$.
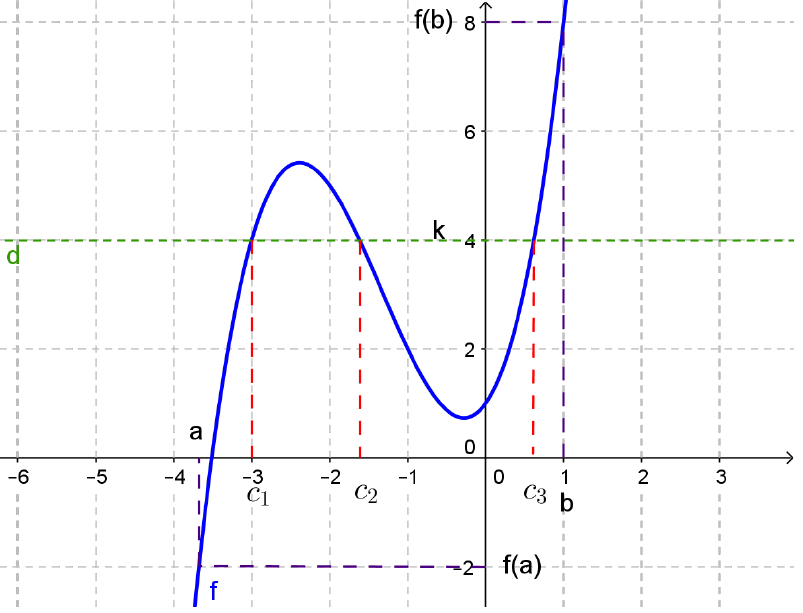
Illustration graphique
La fonction représentée en bleu est continue sur $I=[a,b]$.
Pour $k$ compris entre $f(a)$ et $f(b)$, on remarque graphiquement qu’il existe un $c_1$ dans $[a,b]$ tel que $f(c_1)=k$.
On voit, aussi qu’il existe deux autres $c_2$ et $c_3$ dans $[a,b]$ tels que $f(c_2)=k$ et $f(c_3)=k$. (D’où, dans le théorème, l’importance de l’expression “au moins”)
Cas des fonctions strictement monotones
Soit $f$ une fonction continue et strictement monotone sur un intervalle $[a,b]$ avec $a\leqslant b$.
Pour tout réel $k$ compris entre $f(a)$ et $f(b)$, il existe un unique réel $c$ compris entre $a$ et $b$ tel que $f(c)=k$.
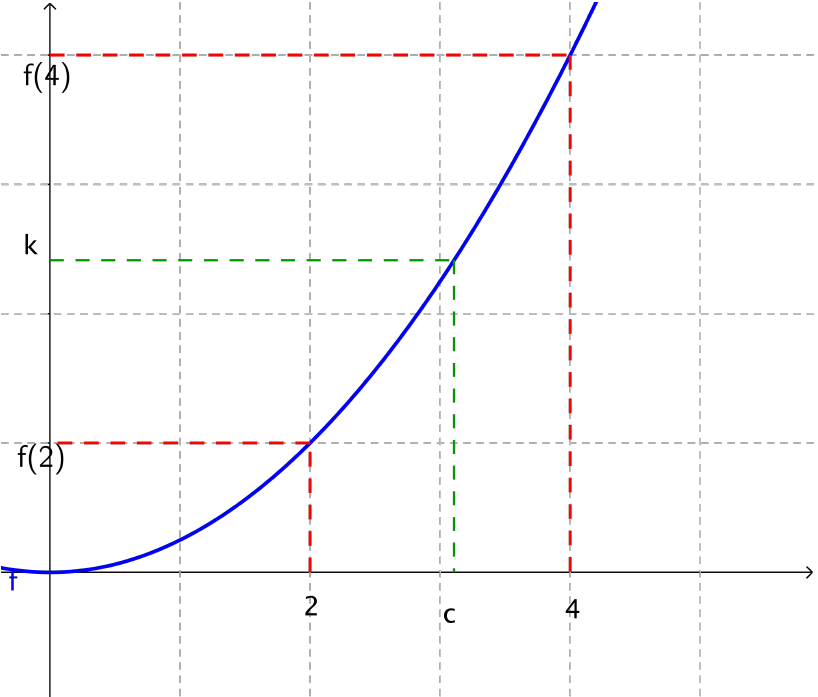
Illustration graphique
La fonction représentée en bleu est continue et strictement croissante sur $I=[2,4]$.
Pour $k$ compris entre $f(2)$ et $f(4)$, on remarque graphiquement qu’il existe un unique $c$ dans $[2,4]$ tel que $f(c)=k$.
La boucle Tant que
La boucle Tant que
Lors de certains algorithmes, il est possible d’utiliser des boucles dont on ignore le nombre de répétitions : ce sont les boucles Tant que.
Exemple :
on dispose d’une population d’individus de 3000 habitants qui augmente chaque année de 2%.
On se demande au bout de combien d’années la population aura dépassé 4000 habitants mais on ignore le nombre d’années : on utilise donc une boucle Tant que.
On écrit donc un algorithme qui permettra de trouver le nombre d’années $N$ pour que la population $P$ dépasse 4000.
- Variables : $N, P$
- Entrée : $3000 \to P$
$0 \to N$
- Traitement : (on traduit la question avec un boucle)
Tant que $P < 4000$ (on souhaite connaitre l’année où la population dépasse 4000 habitants donc tant qu’elle est inférieure à 4000 on continue les calculs et on arrête la première fois qu’elle dépasse 4000).
$ P + 0,02P \to P$
$N + 1 \to N$
Fin Tant que
- Sortie : Afficher $N$
Sans les commentaires, l’algorithme est :
Variables : $N, P$
Entrée : $3000 \to P$
$0 \to N$
Traitement : Tant que $P < 4000$
$P + 0,02P \to P$
$N + 1 \to N$
Fin Tant que
Sortie : Afficher $N$
On peut regarder les différentes valeurs que prennent $N$ et $P$ au début et à la fin de l’algorithme.
Ainsi, au bout d’un an, la population atteint 3060 habitants, $P = 3060$ et $N=1$.
Or $P < 4000$, on continue donc les calculs.
Au bout de 14 années, la population vaut environ $P \approx 3958$.
Mais un an plus tard, au bout de 15 ans, la population vaut $P \approx 4037 > 4000$.
On ne rentre donc plus dans la boucle Tant que et on affiche la valeur de $N$ c’est à dire 15.
Ainsi, il aura fallu 15 ans pour que la population dépasse 4000 habitants.
Le tableau d’avancement du programme est le suivant :
| $P$ | $N$ |
| 3000 | 0 |
| 3060 | 1 |
| $\vdots$ | $\vdots$ |
| $\approx 3958$ | 14 |
| $\approx 4037$ | 15 |