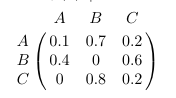Les suites géométriques
Définition
Soit $q$ un réel et $(u_n)_{n\in\mathbb{N}}$ une suite à valeurs réelles.
On dit que $(u_n)$ est une suite géométrique si, et seulement si :
Pour tout $n\in\mathbb{N}$ : $u_{n+1}=q\times u_n$
$ u_0 \underset{\times q}{\longrightarrow} u_1 \underset{\times q}{\longrightarrow} u_2 \underset{\times q}{\longrightarrow} \cdots \underset{\times q}{\longrightarrow} u_{n-1}\underset{\times q}{\longrightarrow} u_n \underset{\times q}{\longrightarrow} u_{n+1}$
On dit alors que $q$ est la raison de la suite géométrique $(u_n)$ et $u_0$ son premier terme.
Expression de $u_n$ en fonction de $n$
Soit $(u_n)$ une suite géométrique de raison $q$.
Si $u_0$ est le premier terme de la suite $(u_n)$, on peut démontrer facilement par récurrence que pour tout $n\in\mathbb{N}$,
$u_n=u_0\times q^n$.
On peut encore écrire cette égalité de la manière suivante :
$u_n=u_p\times q^{n-p}$ avec $p\leqslant n$.
Somme de termes consécutifs
On souhaite calculer la somme de termes consécutifs d’une suite géométrique $(u_n)$.
La somme se calcule de la manière suivante :
$\text{Somme}=\text{(1er terme)} \times \dfrac{1-q^{\text{nombre de termes}}}{1-q}$
Vocabulaire sur les matrices
Vocabulaire sur les matrices
Définition
Une matrice $(n\times p)$ est un tableau à $n$ lignes et $p$ colonnes.
Exemple
$A=\begin{pmatrix}
3 & 4 & -1 \\
0 & \dfrac{1}{2} & 7\\
\end{pmatrix} $ est une matrice $(2\times 3)$
Chaque nombre de $A$ est appelé coefficient: par exemple ${a}_{1;2}=4$ est le coefficient de la première ligne et de la deuxième colonne.
Vocabulaire
Matrice carrée: matrice ayant autant de lignes que de colonnes.
Matrice ligne: matrice ayant une ligne et plusieurs colonnes.
Matrice colonne: matrice ayant une colonne et plusieurs lignes.
Matrice unité:
$I_3=\begin{pmatrix}
1 & 0 & 0 \\
0 & 1 & 0\\
0 & 0 & 1\\
\end{pmatrix} $.
$I_3$ est une matrice carrée de dimension $3$. Ses coefficients valent $1$ sur la diagonale principale et $0$ ailleurs.
Comment montrer qu'une suite est géométrique ?
Comment montrer qu’une suite est géométrique ?
Afin de montrer qu’une suite $(u_n)$ est géométrique, on commence par calculer les premiers termes en s’assurant qu’ils ne sont pas nuls puis on calcule les rapports des premiers termes : $\dfrac{u_1}{u_0}$ et $\dfrac{u_2}{u_1}$.
Considérons par exemple la suite $u_n = 4 \times 3^n$. On a alors $\dfrac{u_1}{u_0} = 3$ et $\dfrac{u_2}{u_1} = 3$.
Si il apparait que le rapport des premiers termes est une constante $q$: on émet alors une conjecture en supposant que la constante ainsi trouvée est la raison de la suite.
Il faut alors montrer en revenant à la définition d’une suite géométrique que $u_{n + 1} = q \times u_n$ pour tout $n \in \mathbb{N}$.
En revenant à notre exemple, on souhaite montrer que $u_{n + 1} = 3 u_n$.
Or :
$3 u_n = 3 \times ( 4 \times 3^n ) $
$3 u_n= 4 \times 3^{n + 1} $
$3 u_n= u_{n + 1}$.
Donc $(u_n)$ est une suite géométrique de raison $3$ et de premier terme $u_0 = 4 \times 3^0 = 4 \times 1 = 4$.
Les graphes probabilistes
Les graphes probabilistes
Les graphes probabilistes permettent de transformer une étude probabiliste en un graphe et sa matrice.
Il existe des graphes d’ordre 2 ou d’ordre 3.
Les poids sur chaque arc correspondent à la probabilité de passer d’un événement à un autre en suivant le sens de parcours imposé par la flèche.
La somme des probabilités inscrites sur les arcs partant d’un événement doit être égale à 1.
Exemples :
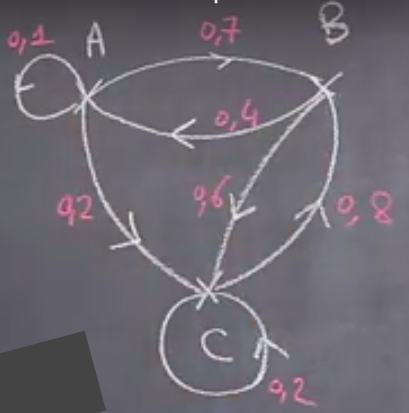
On considère le graphe d’ordre 3 suivant, et on le représente également par une matrice, contenant à l’intersection de la ligne $i$ avec la colonne $j$ la probabilité pour passer de l’événement $i$ à l’événement $j$.
En additionnant les probabilité d’une ligne, on vérifie que le résultat vaut 1.
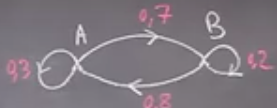
On peut aussi considérer un graphe d’ordre 2.
$M = \left ( \begin{array}{cc} 0.3 & 0.7 \\ 0.8 & 0.2 \end{array} \right )$
Application :
On suppose que la situation que l’on étudie se traduit par le graphe d’ordre 2 précédent, que l’on peut traduire sous forme matricielle.
On considère un état $P_0 = (a \ \; b)$ initial. Pour connaitre l’état $P_1$, on multiplie $P_0$ par $M$ et ainsi de suite.
On trouve alors que pour tout $n \in \mathbb{N}, \ P_{n + 1} = P_n \times M$.
L’état $n + 1$ correspond à l’état $n$ multiplié par la matrice $M$.
Il s’agit d’une suite géométrique de raison $M$ et de terme initial $P_0$.
Ainsi, pour tout $n \in \mathbb{N}, P_n = P_0 \times M^n$. On veillera à ce que l’énoncé donne un premier terme pour $n = 0$.
On essaie de savoir si en regardant pour des états $n$ lointains, le comportement de $P_n$ atteint un état stable, c’est à dire qu’il ne bouge plus, ou encore si la suite $(P_n)$ converge.
Or si aucun des 4 coefficients n’est égal à 0, il existe un état stable, que l’on appelle $P = (x \ \ y)$.
Pour connaitre les valeurs de $x$ et $y$, on sait que la somme des probabilités vaut $1$ et comme il s’agit d’un état stable, il ne change pas lorsque on le multiplie pat la matrice $M$.
On obtient alors le système suivant : $\left \{ \begin{array}{c} PM = P \\ x + y = 1 \end{array} \right.$