Les suites géométriques
Définition
Soit $q$ un réel et $(u_n)_{n\in\mathbb{N}}$ une suite à valeurs réelles.
On dit que $(u_n)$ est une suite géométrique si, et seulement si :
Pour tout $n\in\mathbb{N}$ : $u_{n+1}=q\times u_n$
$ u_0 \underset{\times q}{\longrightarrow} u_1 \underset{\times q}{\longrightarrow} u_2 \underset{\times q}{\longrightarrow} \cdots \underset{\times q}{\longrightarrow} u_{n-1}\underset{\times q}{\longrightarrow} u_n \underset{\times q}{\longrightarrow} u_{n+1}$
On dit alors que $q$ est la raison de la suite géométrique $(u_n)$ et $u_0$ son premier terme.
Expression de $u_n$ en fonction de $n$
Soit $(u_n)$ une suite géométrique de raison $q$.
Si $u_0$ est le premier terme de la suite $(u_n)$, on peut démontrer facilement par récurrence que pour tout $n\in\mathbb{N}$,
$u_n=u_0\times q^n$.
On peut encore écrire cette égalité de la manière suivante :
$u_n=u_p\times q^{n-p}$ avec $p\leqslant n$.
Somme de termes consécutifs
On souhaite calculer la somme de termes consécutifs d’une suite géométrique $(u_n)$.
La somme se calcule de la manière suivante :
$\text{Somme}=\text{(1er terme)} \times \dfrac{1-q^{\text{nombre de termes}}}{1-q}$
Convergence des suites
Convergence des suites
Définitions
On dit qu’une suite $(u_n)$ à valeurs réelles est majorée par $M$ si, et seulement si pour tout $n\in \mathbb{N}$, $u_n\leqslant M$.
On dit qu’une suite $(u_n)$ à valeurs réelles est minorée par $m$ si, et seulement si pour tout $n\in \mathbb{N}$, $u_n\geqslant m$.
Théorème de la limite monotone
$\bullet$ Toute suite à valeurs réelles croissante et majorée par $M$ est convergente vers $\ell$ avec $\ell \leqslant M$.
$\bullet$ Toute suite à valeurs réelles décroissante et minorée par $m$ est convergente vers $\ell$ avec $\ell \geqslant m$.
Remarque : Le minorant (ou majorant) n’est pas nécessairement la limite de la suite!
Exemple :
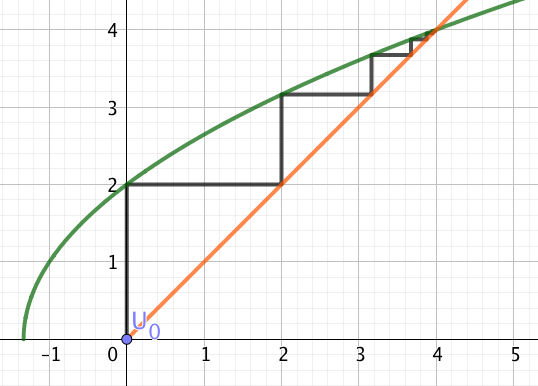
On considère la suite $(u_n)$ définie par récurrence de la manière suivante :
$u_0=0$ et $u_{n+1}=\sqrt{3u_n+4}$
1) Montrer que pour tout $n\in\mathbb{N}$, $u_n\leqslant 4$.
2) Démontrer que $(u_n)$ est une suite croissante.
3) La suite $(u_n)$ est-elle convergente?
Correction
1) On note $\mathcal{P}(n)$ la propriété ” $u_n\leqslant 4$ ” et on va démontrer par récurrence que $\mathcal{P}(n)$ est vraie pour tout $n\in\mathbb{N}$.
Initialisation : on a $u_0=0\leqslant 4$ donc $\mathcal{P}(0)$ est vraie.
Hérédité : on suppose que $\mathcal{P}(n)$ est vraie pour un certain $n\in\mathbb{N}$.
On sait que $u_{n+1}=\sqrt{3u_n+4}$ donc comme par hypothèse de récurrence $u_n\leqslant 4$ on a :
$\sqrt{3u_n+4}\leqslant \sqrt{12+4}=4$ c’est-à-dire $u_{n+1}\leqslant 4$.
Ainsi $\mathcal{P}(n+1)$ est vraie et la récurrence est établie.
2) On a, pour tout $n\in \mathbb{N}, u_{n+1}=f(u_n)$ avec $f:x\mapsto \sqrt{3x+4}$ et on sait que $0\leqslant u_n\leqslant 4$.
Il suffit donc d’étudier les variations de la fonction $f$ sur $[0,4]$ pour trouver les variations de la suite $(u_n)$.
Or la fonction $f$ est la composée de deux fonctions croissantes (racine carrée et une fonction affine à pente positive) donc $f$ est croissante.
Il en résulte donc que la suite $(u_n)$ est croissante.
3) D’après le théorème de la limite monotone, comme $(u_n)$ est croissante et majorée par $4$, elle est convergente et en notant $\ell$ sa limite, on a $0\leqslant \ell \leqslant 4$
Raisonnement par récurrence
Raisonnement par récurrence
Principe
Considérons une chaîne de dominos, faire tomber un domino entraîne son plus proche voisin dans sa chute et ainsi de suite.
Le raisonnement par récurrence utilise ce principe. Il existe des conditions pour que l’ensemble des dominos tombe.
Il faut, dans un premier temps, pousser le premier domino et dans un second temps, il faut être certain que la chute de n’importe quel domino entraîne le suivant.
Mathématiquement, $P_n$ désigne une proposition qui dépend d’un entier naturel $n$ et on souhaite démontrer que $P_n$ est vraie.
Le raisonnement par récurrence se divise en deux parties.
I. Initialisation
La première est l’initialisation : il faut vérifier que $P_0$ ou $P_1$ est vraie c’est-à-dire que la propriété est vraie pour $n=0$ ou $n=1$ (et par analogie, il faut pousser le premier domino).
II. Hérédité
La deuxième est l’hérédité : on suppose que $P_n$ est vraie pour un certain $n$ et on démontre que $P_{n + 1}$ est vraie (par analogie, on considère que le $n^\text{ème}$ domino tombe et on cherche à savoir si le domino suivant, le $(n + 1)^\text{ème}$, tombe également).
En ayant prouvé ces deux parties, cela prouve l’ensemble de la propriété pour tout entier $n$ (tous les dominos tombent).
Comment montrer qu'une suite est géométrique ?
Comment montrer qu’une suite est géométrique ?
Afin de montrer qu’une suite $(u_n)$ est géométrique, on commence par calculer les premiers termes en s’assurant qu’ils ne sont pas nuls puis on calcule les rapports des premiers termes : $\dfrac{u_1}{u_0}$ et $\dfrac{u_2}{u_1}$.
Considérons par exemple la suite $u_n = 4 \times 3^n$. On a alors $\dfrac{u_1}{u_0} = 3$ et $\dfrac{u_2}{u_1} = 3$.
Si il apparait que le rapport des premiers termes est une constante $q$: on émet alors une conjecture en supposant que la constante ainsi trouvée est la raison de la suite.
Il faut alors montrer en revenant à la définition d’une suite géométrique que $u_{n + 1} = q \times u_n$ pour tout $n \in \mathbb{N}$.
En revenant à notre exemple, on souhaite montrer que $u_{n + 1} = 3 u_n$.
Or :
$3 u_n = 3 \times ( 4 \times 3^n ) $
$3 u_n= 4 \times 3^{n + 1} $
$3 u_n= u_{n + 1}$.
Donc $(u_n)$ est une suite géométrique de raison $3$ et de premier terme $u_0 = 4 \times 3^0 = 4 \times 1 = 4$.