Bilan thermique du système Terre-atmosphère - Partie 1
I. Flux d’énergie solaire
Le soleil émet de l’énergie en permanence dans toutes les directions. Sauf que, comme la Terre est loin du soleil, on a vu que les rayons lumineux étaient modélisés par des rayons parallèles les uns aux autres vers la Terre.
Si on met en capteur de 1m2, perpendiculaire aux rayons, on mesure alors un flux de 1360 W. On peut aussi définir le flux surfacique $\phi$ qui est le flux par unité de surface. Comme on a utilisé un capteur de 1m2, le flux surfacique du soleil sur la distance Terre-soleil est de $1360W.m^{-2}$. On appelle cela la constante solaire. Mais quel est le flux capté par la Terre ?
II. Flux d’énergie reçue par la Terre
Il faut se demander quelle surface les rayons vont couper ? Si on regarde la Terre de face, on voit un disque. C’est donc ce disque qui va être coupé par les rayons lumineux. Les rayons déposent de l’énergie sur un disque qui possède le rayon de la Terre.
La surface est donc de : $\pi \times R_T^2$.
Donc, le flux total reçu par la Terre c’est : $\phi_{total \ reçu} = \phi \times \pi R_T^2$.
Ce flux est exprimé en Watts, c’est une puissance.
III. Flux surfacique à la surface de la Terre (au sommet de l’atmosphère)
Le flux total qui arrive se réparti de manière homogène sur toute la surface de la Terre. Il y a deux cercles concentriques :
– le cercle dont le rayon est le plus petit correspond à la surface terrestre,
– le cercle dont le rayon est le plus grand est la surface atmosphérique.
On a appelé $R_T$ le rayon de la Terre et $e$ l’épaisseur de l’atmosphère. Le rayon de la Terre est d’environ 6 400 km et l’épaisseur de l’atmosphère est d’environ 500 km. On peut donc négliger $e.$ Quand on parle de flux surfacique au sommet de l’atmosphère c’est la même chose que le flux surfacique à la surface de la Terre.
On fait l’hypothèse que la distance entre le centre de la Terre et le sommet de l’atmosphère est égale à $R_T$. La surface totale sur laquelle se réparti le flux est la surface de la Terre : $4\times \pi \times R_T^2$.
Soit $\phi_S$ le flux surfacique au sommet de l’atmosphère, $\phi_s = \dfrac{\phi_{total \ reçu}}{4\pi R_T^2} = \dfrac{\phi}{4} = 340W.m^{-2}$.
Bilan thermique du système Terre-atmosphère - Partie 2
Au sommet de l’atmosphère, le flux surfacique est de $340W.m^{-2}$.
I. Albédo
L’albédo est le coefficient de réflexion du flux d’énergie. Il y a un flux $\phi_i$ incident qui arrive sur Terre et un flux $\phi_r$ réfléchi qui part de la Terre.
L’albédo est un coefficient sans unité qui intervient dans la formule suivante : $\phi_r = a\times \phi_i$.
Les flux d’énergie incidents et réfléchis sont en Watts. Cette relation est la même pour les flux surfaciques.
L’albédo est forcément plus petit que 1 puisqu’on ne peut pas avoir une énergie plus grande que l’énergie incidente.
Par exemple, la neige a un albédo de 0,9. Le flux réfléchi est égal à 0,9 fois le flux incident. Autrement dit : 90 % de l’énergie incidente sur la neige est réfléchie. L’albédo total moyen de la Terre est de 0,3. C’est l’albédo qui permet de relier le flux incident qui arrive au sommet de l’atmosphère au flux réfléchi qui quitte la Terre, au sommet de l’atmosphère.
$\phi_r = 0,3 \times \phi_i = 100W.m^{-2}$. C’est le flux surfacique moyen sur Terre.
II. Loi de Stefan Boltzmann
C’est une loi qui permet de calculer la température d’un corps noir à partir du flux surfacique émis par ce corps noir. Les étoiles sont souvent modélisées comme des corps noirs. Même un four avec un petit trou pourrait être modélisé comme un corps noir.
Un corps noir est un élément qui possède une certaine température et qui émet un flux lumineux. La Terre, elle-aussi, émet un flux lumineux mais ce n’est pas de la lumière visible.
Faisons l’hypothèse que la Terre est un corps noir : on peut calculer à quel flux surfacique d’émission cela correspond. La température moyenne sur Terre est de 15° C donc 288 K. On a donc la formule suivante qui peut être utilisée :
$\phi = \sigma \times T^4$
Par conséquent, le flux surfacique émis est de $390W.m^{-2}$.
Dans la formule, sigma est la constante de Boltzmann et vaut 5,67.10^{-7}W.m^{-2}.K^{-4}$.
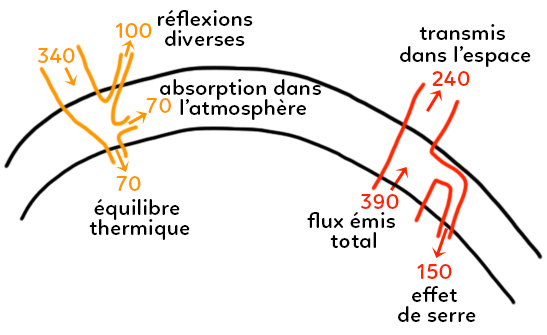
III. Schéma des flux d’énergies
Le trait extérieur noir et le sommet de l’atmosphère, celui en dessous est la surface de la Terre. Il y a différents canaux d’énergie. Chaque canal d’énergie présente des valeurs. Ce sont les flux surfaciques en $W.m^{-2}$.
On dit qu’il n’y a pas d’effet de serre et on ne prend que la partie gauche du schéma. On a un flux incident de $340W.m^{-2}$ à la surface. On a un flux réfléchi de $100 W.m^{-2}$. Cela correspond à diverses réflexions : les nuages, l’atmosphère, etc. Le reste passe et on va avoir $170 W.m^{-2}$ absorbés par la surface de la Terre et $70 W.m^{-2}$ absorbés dans l’atmosphère. $240 W.m^{-2}$ sont, en fait, absorbés par la Terre.
Dans le cas de l’équilibre thermique, on a $240 W.m^{-2}$ absorbés par la Terre et également $240 W.m^{-2}$ émis. C’est ce qui permet que la Terre ne surchauffe pas, bien plus que pour le réchauffement climatique d’ailleurs.
On peut utiliser la formule de Boltzmann : $T = (\dfrac{\phi}{\sigma})^{1/4} = 255 K$ soit -18° C.
On va donc imposer d’avoir un flux émis total de $390 W.m^{-2}$, comme calculé plus haut. Par contre, il manque $150 W.m^{-2}$ pour atteindre l’équilibre thermique. Ces $150 W.m^{-2}$ viennent de l’effet de serre.
Dans l’atmosphère, certaines molécules vont absorber les rayonnements et les réémettre : les gaz à effets de serre comme le CO2 par exemple. $240 W.m^{-2}$ sont bien émis dans l’espace. Entre le sol de la Terre et le sommet de son atmosphère, l’équilibre thermique est présent. L’effet de serre est donc nécessaire pour garder l’équilibre thermique et la température moyenne de 15° C sur Terre.