Cercle trigonométrique, longueur d'arc radian
Cercle trigonométrique, longueur d'arc radian
Cercle trigonométrique – longueur d’arc – radian
I – Cercle trigonométrique et longueur d’arc
Définition :
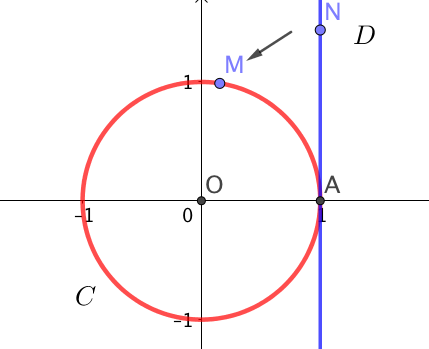
On appelle cercle trigonométrique noté $\mathcal{C}(O; 1)$ le cercle de centre $O$ et de rayon 1, orienté dans le sens direct (c’est à dire le sens anti-horaire ou bien le sens inverse des aiguilles d’une montre).
Son périmètre vaut $P = D \times \pi = 2 \pi$.
On trace la droite des réels tangente au cercle trigonométrique au point $(1;0)$.
Par enroulement de la droite réelle $\mathcal{D}$ sur le cercle trigonométrique, on obtient les résultats suivants :
– A tout réel $x$ de la droite et en notant $N$ le point correspondant, on associe un point $M$ unique sur ce cercle.
La longueur de l’arc $\overset{\frown}{AM}$ est exactement égale à la longueur $AN$.
– A tout point $M$ du cercle est associé une infinité de réels.
En effet, si $x$ est un réel, on obtient un autre réel sur la droite en écrivant $x + 2k \pi$, avec $k$ entier. Cela vient du fait que l’on peut enrouler plusieurs fois la droite sur le cercle et donc repasser une infinité de fois en un point donné du cercle.
En outre, la longueur du cercle correspondant au périmètre et valant donc $2\pi$, un tour de cercle correspond donc à ajouter $2\pi$.
On dira alors que $x$ est défini modulo $2\pi$.
II) Une nouvelle mesure d’angle
Définition :
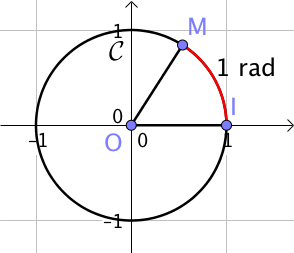
Un radian est la mesure d’un angle orienté $\widehat{IOM}$ interceptant un arc de 1 unité sur le cercle trigonométrique.
Remarque :
La longueur d’un arc et la mesure de l’angle qui l’intercepte sont proportionnelles.
Il y a donc proportionnalité entre les degrés et les radians.
La mesure de l’angle plein, c’est à dire 360°correspond à l’arc complet, c’est à dire $2 \pi$.
On peut compléter le tableau de proportionnalité suivant, qui donne la correspondance entre les degrés et les radians.
| Degré | 360° | 180° | 90° | 45° | 30° | 60° | 0° |
| Radian | $2\pi$ | $\pi$ | $\dfrac{\pi}{2}$ | $\dfrac{\pi}{4}$ | $\dfrac{\pi}{6}$ | $\dfrac{\pi}{3}$ | 0 |
Application :
Donner la mesure en radian d’un angle de 35°.
On utilise donc le tableau de proportionnalité de correspondance entre les degrés et les radians.
| Degré | 360° | 35° |
| Radian | $2\pi$ | ? |
Ainsi la valeur en radian est donnée par le calcul suivant :
$\dfrac{35 \times 2 \pi}{360} = \dfrac{7 \times 5 \times 2\pi}{36 \times 10} = \dfrac{7\pi}{36}$