Ajustement par changement de variable
Ajustement par changement de variable
Ajustement par changement de variable
Lorsque le nuage de points d’une série statistique à deux variables a une forme exponentielle, il est possible d’effectuer un changement de variable pour se ramener à une trajectoire rectiligne que l’on peut ajuster à l’aide de la méthode des moindres carrés.
Méthode :
On pose $z = \ln y$ et les fonctions exponentielle et logarithme sont réciproques l’une de l’autre. Il faut cependant veiller à la positivité des valeurs pour pouvoir appliquer la fonction logarithme.
La calculatrice fournit alors l’équation de la droite de régression linéaire :
$z = ax + b$
$\iff \ln y = ax + b$
$\iff e^{\ln y} = e^{ax + b}$
$\iff y = e^{ax + b}$
Exemple :
On étudie le nombre de like en fonction du nombres d’abonnés sur Instagram.
|
nombre de like en milliers |
12 | 36 | 53 | 62 | 72 | 80 |
|
nombres d’abonnés sur Instagram en dizaines de milliers |
20 | 25 | 31 | 40 | 68 | 99 |
Le but de l’exercice est de déterminer le nombre d’abonnés que l’on pourrait obtenir si la prochaine vidéo obtenait 100 000 like.
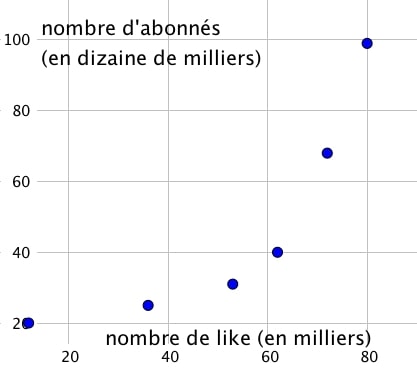
On commence tout d’abord par tracer le nuage de points de la série statistique.
On peut alors remarquer que la trajectoire est exponentielle.
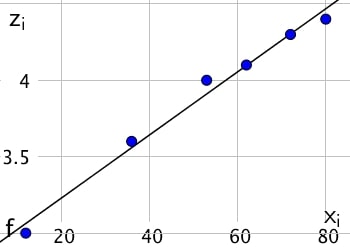
On pose donc $z = \ln y$
CALCUL DES LN FAUX
| $x_i$ | 12 | 36 | 53 | 62 | 72 | 80 |
| $z_i = \ln y_i$ | 3 | 3,2 | 3,4 | 3,7 | 4,2 | 4,6 |
A l’aide de la calculatrice, on obtient $z = 0.02x + 2.50$ et $r \approx 0.92$.
Le coefficient de corrélation linéaire est proche de $1$ donc l’approximation par la droite de régression linéaire est pertinente.
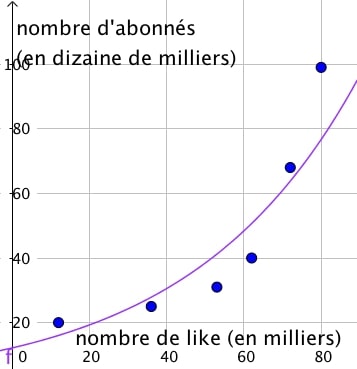
Comme $z = 0.023x + 2.50$ alors $ e^{\ln y} = e^{0.023x + 2.50}$ c’est à dire $y = e^{0.023x} \times e^{2.50} \approx 12.18e^{0.023x}$.
Finalement, on cherche le nombre d’abonnés lorsque la vidéo obtient 100 000 like, c’est à dire $x = 100$ ($x$ s’exprime en milliers) : $y = 12.18e^{0.023 \times 100} = 110$.
D’après ce modèle, on obtient 1,10 millions d’abonnés.