Chute d'un objet sans vitesse - Étape 1 : Système, référentiel et bilan des forces
Chute d'un objet sans vitesse - Étape 1 : Système, référentiel et bilan des forces
Étape 1 : système, référentiel et Bilan des forces
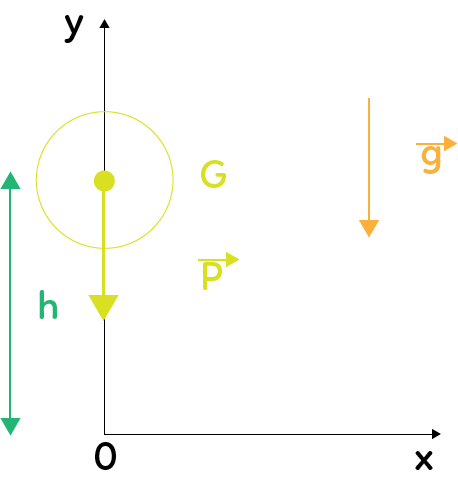
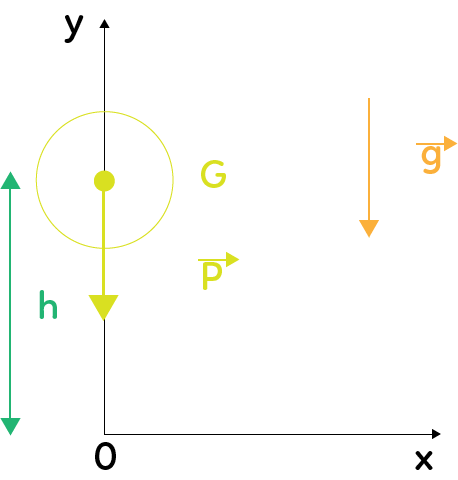
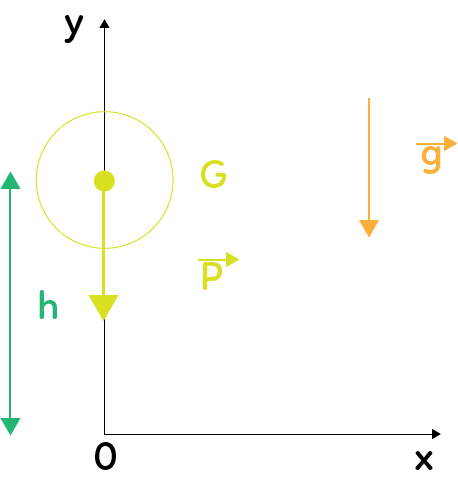
Il s’agit d’un objet, d’une balle par exemple, de centre $G$ placé dans un repère bidimensionnel ($Ox, Oy$) ascendant.
Au voisinage de la surface de la Terre règne un champ de pesanteur uniforme représenté par le vecteur $\overrightarrow{g}$.
Il faut prêter une attention particulière aux conditions initiales. Ici, on suppose que la balle est lâchée sans vitesse initiale.
La première étape consiste à déterminer le système d’étude : la balle, de masse $m$.
On définit dans un second temps le référentiel d’étude : le référentiel terrestre, puisque la balle est au voisinage de la Terre, que l’on suppose galiléen c’est-à-dire un référentiel dans lequel on peut appliquer les trois lois de Newton.
Enfin, on réalise le bilan des forces agissant sur l’objet d’étude. Ici, la seule action mécanique modélisée par le vecteur $\overrightarrow{P}$ à laquelle est soumise la balle est le poids (vertical vers le bas), en négligeant les frottements de l’air, c’est-à-dire en se plaçant dans des conditions idéales qui n’ont pas de réalité physique.
On peut alors appliquer la deuxième loi de Newton, qui stipule que :
$\sum \overrightarrow{F_{ext}} = m \times \overrightarrow{a} = \dfrac{\text{d}\overrightarrow{p}}{\text{dt}}$,
ou encore que la somme des forces extérieures à la balle agissant sur la balle est égale au produit de la masse de la balle par l’accélération de cette dernière ou à la dérivée de la quantité de mouvement de la balle par rapport au temps, ces deux relations étant équivalentes.
D’après le bilan des forces, la somme des forces extérieures est égale au poids :
$\overrightarrow{P} = m \times \overrightarrow{a}$ ou encore $m\times \overrightarrow{g} = m \times \overrightarrow{a}$ et finalement : $\overrightarrow{a} = \overrightarrow{g}$.
Chute d'un objet sans vitesse - Étape 2 : Les coordonnées du vecteur accélération
Étape 2 : les coordonnées du vecteur accélération
On souhaite suivre le mouvement de la balle, lâchée sans vitesse initiale, au cours du temps.
On a établi précédemment, grâce à la deuxième loi de Newton, que $\overrightarrow{a} = \overrightarrow{g}$.
On peut décomposer le vecteur accélération en donnant ses coordonnées. On a donc $\overrightarrow{a} \left ( \begin{array}{c} a_x \\ a_y \\ \end{array} \right ) $.
De même, on retrouve facilement les coordonnées du vecteur champ de pesanteur : $\overrightarrow{g} \left ( \begin{array}{c} 0 \\ -g \\ \end{array} \right ) $, avec $g = 9,81 \text{m.s}^{-2}$, car on a choisi un axe $Oy$ ascendant.
Si deux vecteurs sont égaux, alors leurs coordonnées sont égales deux à deux :
$ \left\{
\begin{array}{ccc}
a_x & = & 0 \\
a_y & = & -g \\
\end{array}
\right.$
On a trouvé les coordonnées du vecteurs accélération quel que soit le temps.
Pour déterminer le vecteur vitesse, il faut se remémorer le lien entre accélération et vitesse :
$\overrightarrow{a} = \dfrac{\text{d}\overrightarrow{v}}{\text{dt}}$. Les coordonnées du vecteur vitesse doivent être égales, une fois dérivés, aux coordonnées du vecteur accélération ; on doit donc trouver des primitives des coordonnées du vecteur accélération.
Ainsi, la première coordonnée du vecteur vitesse, $v_x$, doit être égale, après dérivation, à $0$ : c’est une constante notée $C_1$.
De même, la deuxième composante du vecteur vitesse, $v_y$, doit être égale, après dérivation par rapport au temps , à $-g$, ainsi $v_y = -g \times t + C_2$. Lorsque l’on trouve une primitive, il ne faut pas oublier d’ajouter une constante, car la dérivée d’une constante vaut $0.$
A partir des conditions initiales, il sera possible de déterminer la valeur des constantes.
Chute d'un objet sans vitesse - Étape 3 : Les coordonnées du vecteur vitesse
Étape 3 : les coordonnées du vecteur vitesse
Il a été trouvé précédemment, en primitivant les coordonnées du vecteur accélération, que $\overrightarrow{v}$ s’écrit sous la forme :
$ \left\{
\begin{array}{ccc}
v_x & = & C_1 \\
v_y & = & -gt + C_2 \\
\end{array}
\right.$
Il s’agit donc de déterminer totalement la vitesse en trouvant la valeur des constantes grâce aux conditions initiales, c’est-à-dire au moment où on lâche la balle à $t = 0$. A $t = 0$, la balle n’avait pas de vitesse initiale, ainsi, $\overrightarrow{v}(t = 0) = \overrightarrow{0}$; il faudra faire attention à écrire une égalité vectorielle.
Or en se plaçant à $t = 0$ s et en remplaçant donc $t$ par $0$ dans les coordonnées de la vitesse on obtient une nouvelle information sur $\overrightarrow{v}(t = 0)$ qui est alors égal à $ \left\{
\begin{array}{ccccc}
v_x & = & C_1 & = & 0\\
v_y & = & -g \times 0 + C_2 = C_2 & = & 0 \\
\end{array}
\right.$
Une fois les constantes $C_1$ et $C_2$ déterminées, le vecteur vitesse est totalement déterminé et vaut pour tout instant $t$ : $ \left\{
\begin{array}{ccc}
v_x & = &0 \\
v_y & = & -gt \\
\end{array}
\right.$
Il faut maintenant trouver les coordonnées du vecteur position $\overrightarrow{OG}$, avec $O$ l’origine du repère et $G$ le centre de la balle à chaque instant, défini par $\overrightarrow{v} = \dfrac{\text{d}\overrightarrow{OG}}{\text{dt}}$, soit en d’autres termes le vecteur vitesse est la dérivée par rapport au temps du vecteur position.
Chute d'un objet sans vitesse - Étape 4 : Les coordonnées du vecteur position
Étape 4 : les coordonnées du vecteur position
Ayant déterminé précédemment la vitesse de la balle, on souhaite à présent connaitre sa position à chaque instant.
Il faut maintenant déterminer les coordonnées du vecteur position $\overrightarrow{OG}$, avec $O$ l’origine du repère et $G$ le centre de la balle à chaque instant, défini par $\overrightarrow{v} = \dfrac{\text{d}\overrightarrow{OG}}{\text{dt}}$, soit en d’autres termes le vecteur vitesse est la dérivée par rapport au temps du vecteur position.
Pour se faire, il faut trouver des primitives des coordonnées du vecteur vitesse. Une primitive de $v_x$ est une fonction qui une fois dérivée vaut 0 : c’est une constante notée $C_3$.
De même, une primitive de $v_y$ est $-\dfrac{1}{2} \times gt^2 + C_4$. En effet, si on dérive cette expression, on obtient alors $-\dfrac{1}{2} \times 2 \times gt + 0 = -gt $.
Les coordonnées de $\overrightarrow{OG}$ sont donc $ \left\{
\begin{array}{ccc}
x & = & C_3 \\
y & = & -\dfrac{1}{2} \times gt^2 + C_4 \\
\end{array}
\right.$
Pour trouver la valeur des constantes, on utilise à nouveau les conditions initiales.
Ainsi, à $t = 0$, d’après le schéma, on trouve $x(t = 0) = 0$ et $y(t = 0) = h$.
Or, on dispose également des coordonnées de $\overrightarrow{OG}$ pour tout temps $t$, en particulier pour $t = 0$. En remplaçant $t$ par 0 on obtient :
$ \left\{
\begin{array}{ccccc}
x & = & C_3 & = & 0 \\
y & = & -\dfrac{1}{2} \times g \times 0^2 + C_4 = C_4 &=& h \\
\end{array}
\right.$
On raisonne par identification pour trouver la valeur des constantes et on peut remarquer que l’on retrouve bien qu’à $t = 0$, on a lâché la balle d’une hauteur $h$.
Ayant déterminé les constantes $C_3$ et $C_4$, il est possible maintenant de trouver le vecteur position pour tout instant $t$ :
$\overrightarrow{OG} \left\{
\begin{array}{ccc}
x & = & 0 \\
y & = & -\dfrac{1}{2} \times gt^2 + h \\
\end{array}
\right.$
Ce système s’appelle les équations horaires de la balle car elles dépendent du temps et définissent à chaque instant les coordonnées de la balle.