Coefficients binomiaux - Définition
Coefficients binomiaux
On considère un schéma de Bernoulli de paramètres $n$ (le nombre de répétitions) et $p$ (la probabilité du succès).
Soit $k$ un entier tel que $0 \leq k \leq n$.
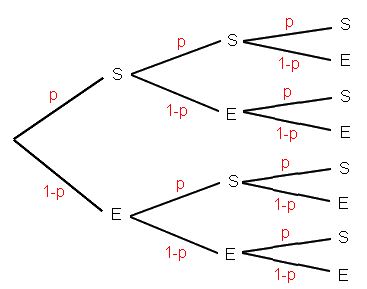
Le coefficient binomial noté $\left ( \begin{array}{c} n \\ k \end{array} \right ) $, que l’on lit $k$ parmi $n$, est égal au nombre de chemins conduisant à $k$ succès “S” dans l’arbre pondéré représentant le schéma de Bernoulli.
Exemple :
Considérons $n = 3$ et $k = 2$. ($0 \leq k \leq 3$)
On cherche à calculer 2 parmi 3, c’est à dire $\left ( \begin{array}{c} 3 \\ 2 \end{array} \right ) $.
On doit donc compter le nombre de chemins contenant 2 succès : il y a 3 chemins.
Ainsi $\left ( \begin{array}{c} 3 \\ 2 \end{array} \right ) = 3$.
De même, $\left ( \begin{array}{c} 3 \\ 1 \end{array} \right ) = 3$.
Ou encore $\left ( \begin{array}{c} 3 \\ 0 \end{array} \right ) = 1$ car il n’y a qu’un chemin avec 0 succès (et donc 3 échecs).
Coefficients binomiaux - Propriétés
Coefficients binomiaux – Propriétés
Propriétés :
1) Pour tout $n \in \mathbb{N},$
$\left ( \begin{array}{c} n \\ 0 \end{array} \right ) = 1$ car cela correspond au chemin où il n’y a que des échecs, et il n’y en a qu’un seul.
$\left ( \begin{array}{c} n \\ n \end{array} \right ) = 1$ car cela correspond au chemin où il n’y a que des succès, et il n’y en a qu’un seul.
$\left ( \begin{array}{c} n \\ 1 \end{array} \right ) = n$
2) Pour tout $n \in \mathbb{N}$ et $0 \leq k \leq n$
$\left ( \begin{array}{c} n \\ n – k \end{array} \right ) = \left ( \begin{array}{c} n \\ k \end{array} \right ) $, c’est une propriété de symétrie.
3) Pour tout $n \in \mathbb{N}$ et $0 \leq k \leq n$
$\left ( \begin{array}{c} n \\ k \end{array} \right ) + \left ( \begin{array}{c} n \\ k + 1\end{array} \right ) = \left ( \begin{array}{c} n + 1 \\ k + 1 \end{array} \right ) $
Exemples :
Calculons $\left ( \begin{array}{c} 6 \\ 5 \end{array} \right ) $ qui est égal à $\left ( \begin{array}{c} 6 \\ 6 – 5 \end{array} \right ) = \left ( \begin{array}{c} 6 \\ 1 \end{array} \right ) = 6 $
Calculons $\left ( \begin{array}{c} 4 \\ 2 \end{array} \right ) $ qui est égal à $\left ( \begin{array}{c} 3 + 1 \\ 1 + 1 \end{array} \right )$.
On applique alors la propriété 3) avec $k = 1$ et $n = 3$, $\left ( \begin{array}{c} 6 \\ 5 \end{array} \right ) = \left ( \begin{array}{c} 3 \\ 1 \end{array} \right ) + \left ( \begin{array}{c} 3 \\ 1 \end{array} \right ) = 3 + \left ( \begin{array}{c} 2 + 1 \\ 1 + 1 \end{array} \right )$ (en appliquant les propriétés 1) $ = 3 + \left ( \begin{array}{c} 2 \\ 1 \end{array} \right ) + \left ( \begin{array}{c} 2 \\ 2 \end{array} \right ) = 3 + 2 + 1 $ (en appliquant les propriétés 1) $ = 6 $
La calculatrice permet de calculer directement les coefficients binomiaux.
Triangle de Pascal
Le triangle de Pascal
Le triangle de Pascal permet de trouver les valeurs de $k$ parmi $n$, c’est à dire les coefficients binomiaux.
La première ligne contient les valeurs de $k$ alors que la première colonne contient les valeurs de $n$.
La première colonne ($k = 0$) se remplit à partir de la formule $\left ( \begin{array}{c} n \\ 0 \end{array} \right ) = 1$
La diagonale ($k = n$) se remplit à l’aide de la formule $\left ( \begin{array}{c} n \\ n \end{array} \right ) = 1$.
La deuxième colonne ($k = 1$) se remplit à l’exception de la première case (car $k$ doit être inférieur à $n$) à l’aide de la formule $\left ( \begin{array}{c} n \\ 1 \end{array} \right ) = n$.
Ainsi, par exemple la troisième ligne ($n = 2$) vaut $ \left ( \begin{array}{c} 2 \\ 1 \end{array} \right ) = 2$.
Comme $k$ doit être inférieur à $n$, on ne peut remplir que la partie inférieure du tableau : il apparait alors un triangle.
Pour remplir le reste du tableau, on utilise la formule suivante
$\left ( \begin{array}{c} n \\ k \end{array} \right ) + \left ( \begin{array}{c} n \\ k + 1\end{array} \right ) = \left ( \begin{array}{c} n + 1 \\ k + 1 \end{array} \right ) $.
Cette dernière se traduit par le fait qu’une case correspond à la somme du coefficient de la case du dessus et du coefficient de la case à gauche de cette dernière.
Ainsi, par exemple $\left ( \begin{array}{c} 3 \\ 2 \end{array} \right ) = \left ( \begin{array}{c} 2 \\ 2\end{array} \right ) + \left ( \begin{array}{c}2 \\ 1 \end{array} \right ) = 1 + 2 = 3$
On obtient alors le tableau suivant :
On retrouve la propriété de symétrie des coefficients :
$\left ( \begin{array}{c} n \\ n – k \end{array} \right ) = \left ( \begin{array}{c} n \\ k \end{array} \right ) $.