Comparer deux quantités
Comparer deux quantités
Principe
Comparer deux quantités $A$ et $B$ revient à chercher la plus grande des deux ou conclure qu’elles sont égales.
Il peut y avoir plusieurs méthodes pour comparer deux quantités :
1) On cherche le signe de la différence :
$A > B$ équivaut à $A – B > 0$ et $B – A < 0$.
2) On compare le quotient (de réels positifs) au nombre $1$.
$\left \{ \begin{array}{l} A > B \\ A > 0 \\ B > 0 \\ \end{array} \right.$ équivaut à $\dfrac{A}{B} > 1$ et $ \dfrac{B}{A} < 1$.
Exemple
On souhaite comparer $\dfrac{7}{6}$ et $\dfrac{10}{9}$ en utilisant les deux principes précédents.
a) On commence donc par calculer la différence, en mettant les fractions au même dénominateur.
$\dfrac{10}{9} – \dfrac{7}{6} = \dfrac{10 \times 2}{9 \times 2} – \dfrac{7 \times 3}{6 \times 3} = \dfrac{20}{18} – \dfrac{21}{18} = \dfrac{-1}{18} < 0$.
Donc $\dfrac{10}{9} – \dfrac{7}{6} < 0$, ainsi $\dfrac{10}{9} < \dfrac{7}{6}$.
b) On calcule à présent le quotient des fractions, en vérifiant qu’elles sont bien toutes deux positives.
$\dfrac{\dfrac{10}{9}}{\dfrac{7}{6}} = \dfrac{10}{9} \times \dfrac{6}{7} = \dfrac{60}{63}$.
Le numérateur étant plus petit que le dénominateur, $\dfrac{60}{63} < 1$.
Ainsi, $\dfrac{\dfrac{10}{9}}{\dfrac{7}{6}} < 1$ donc $\dfrac{10}{9} < \dfrac{7}{6}$.
Application
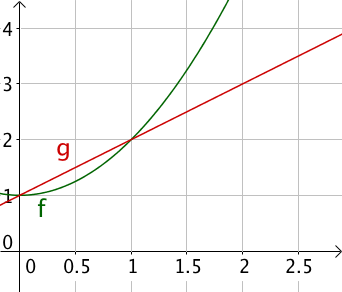
Soient $f$ et $g$ deux fonctions définies pour tout $x \in [0; + \infty [$ par $f(x) = x^2 + 1$ et $g(x) = x + 1$.
On souhaite étudier la position relative de $\mathcal{C}_f$ et $\mathcal{C}_g$, c’est à dire savoir quand $f$ est plus grande que $g$ et inversement.
Pour cela, on calcule la différence :
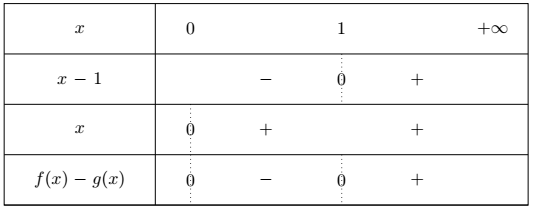
$f(x) – g(x) = x^2 + 1 – (x + 1) = x^2 + 1 – x – 1 = x^2 – x = x(x-1)$.
On préfèrera factoriser l’expression pour simplifier l’étude du signe.
Le premier facteur $x$ est toujours positif sur $[0; + \infty [$ et $(x – 1)$ est négatif pour $ x \in ]0; 1[$ et positif pour $x \geq 1$.
Ainsi $f(x) – g(x) < 0$ pour $x \in ]0; 1[$.
Donc $f(x) < g(x)$ pour $x \in ]0; 1[$.
Ainsi $\mathcal{C}_f$ est en dessous de $\mathcal{C}_g$.
On ne pourra pas écrire que $\mathcal{C}_f$ est inférieure de $\mathcal{C}_g$ mais on dira que $f$ est inférieure à $g$.
Pour $x >1$,
$f(x) – g(x) > 0$ donc $\mathcal{C}_f$ est en dessus de $\mathcal{C}_g$.