La continuité
La continuité
Continuité en un point
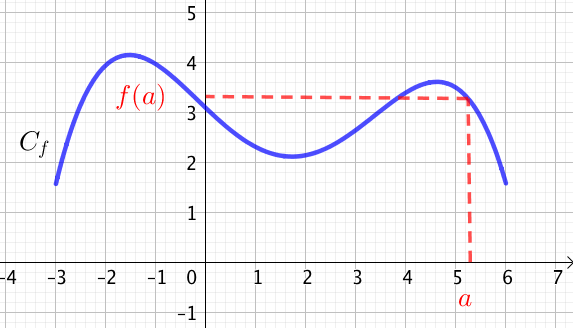
Soit $f$ une fonction définie sur un intervalle $I$ à valeurs dans $\mathbb{R}$ et $a \in I$, $f$ est continue en $a$ si et seulement si $\lim\limits_{x \to a} f(x) = f(a)$.
La fonction $f$ est définie en $a$, $a$ admet donc une image par $f$ qui est $f(a)$. En outre, la limite de la fonction $f$ lorsque $x$ tend vers $a$ doit s’approcher à droite et à gauche de $f(a)$.
Dans certains exercices, il faudra calculer la limite à droite et la limite à gauche de la fonction puis vérifier que ces deux limites valent $f(a)$.
Lorsque l’on trace une fonction $f$ continue sur intervalle $I$, on le fait sans lever le crayon. Il s’agit d’un moyen de se représenter la continuité mais cela ne constitue en rien une définition rigoureuse de cette dernière.
Continuité sur un intervalle
$f$ est continue sur un intervalle $I$ si et seulement si $f$ est continue en chaque réel $a$ de $I$.
Les fonctions polynômes, rationnelles, trigonométriques, logarithmes, exponentielles sont continues sur leur domaine de définition.
La continuité - Fonction partie entière
Étudier la continuité de la fonction \(E(x)\), partie entière de \(x\) sur \(\mathbb{R}\).
Ce qu’il faut savoir faire :
- Étape 1 : Graphiquement on voit que la fonction n’est pas continue.
- Étape 2 : Mathématiquement, les limites à gauche et à droite ne sont pas les mêmes, donc la fonction n’est pas continue.