Vecteur position, vitesse et accélération
Ce sont trois vecteurs qui permettent de décrire un mouvement. En mécanique, le point $M$ va bouger et son mouvement va être décrit par ces trois vecteurs : accélération, position et vitesse. Leur utilisation sera décrite dans le cours sur la deuxième loi de Newton.
I. Vecteur position : $\overrightarrow{OM}$
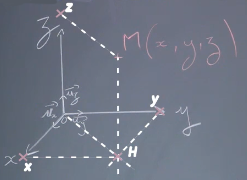
Pour décrire une position dans l’espace, on utilise un repère. Ce repère est un repère à coordonnées cartésiennes $(O ; x ; y ; z).$
Ces trois axes doivent être orthonormés directs. Avec les trois doigts de la main gauche, on peut faire les axes $x, y$ et $z$. On place ensuite le point $M$ de coordonnées $(x ;y ;z).$ Il faut s’entraîner à savoir les tracer au brouillon rapidement. On trace la projection $H$ de $M$ sur le plan $(O ;x ;y ;z).$
Pour cela on descend sur la parallèle à l’axe $z$ partant du point $M.$ On va ensuite tracer du point $H$ une parallèle à l’axe $\overrightarrow{Oy}$ qui coupe l’axe $\overrightarrow{Ox}$. On a la coordonnée $x.$ On trace la parallèle à l’axe $\overrightarrow{Ox}$ qui coupe l’axe $\overrightarrow{Oy}$ en $y.$
Ensuite, on trace une parallèle à $(HO)$ à partir du point $M$ qui coupe l’axe $\overrightarrow{Oz}$. C’est la coordonnée $z.$ Mathématiquement, le vecteur $\overrightarrow{OM}$ peut aussi s’écrire $\overrightarrow{OM} = x\overrightarrow{u_x}+y\overrightarrow{u_y}+z\overrightarrow{u_z}$.
Les vecteurs dans l’expression sont des vecteurs unitaires qui caractérisent un déplacement de $x, y$ et $z$ quantités. On peut écrire les coordonnées du vecteur sous différentes formes.
II. Vecteur vitesse : $\overrightarrow{v}$
S’il n’y a pas de flèche sur le $v$ de la vitesse cela signifie qu’il s’agit de la norme de la vitesse et non du vecteur. On peut aussi y ajouter les barres de valeur absolue. Elle s’exprime en m/s (ou $m.s^{-1}$).
Le vecteur vitesse est la dérivée par rapport au temps du vecteur position : $\overrightarrow{v} = \dfrac{d\overrightarrow{OM}}{dt}$.
On va l’exprimer comme ceci : $\overrightarrow{v} = \dfrac{d}{dt}(x\overrightarrow{ux}+ y\overrightarrow{uy}+ z\overrightarrow{uz} ) = \dfrac{dx}{dt}\overrightarrow{ux}+\dfrac{dy}{dt}\overrightarrow{uy}+\dfrac{dz}{dt}\overrightarrow{uz} = \overrightarrow{v_x}\overrightarrow{ux}+\overrightarrow{v_y}\overrightarrow{uy}+\overrightarrow{v_z}\overrightarrow{uz}$.
On a donc les dérivées qui correspondent aux vitesses en $x, y$ et $z.$ On peut aussi noter les dérivées avec la lettre et un point au-dessus. Si on mettait deux points au-dessus, cela voudrait dire qu’on dérive deux fois par rapport au temps.
Par exemple, on prend un vecteur $\overrightarrow{OM}$ de coordonnée (2t, 3t, h). On veut connaître la vitesse. La vitesse est la dérivée de la position donc le vecteur vitesse a pour coordonnées (2, 3, 0).
On peut aussi l’écrire comme ceci : $\overrightarrow{OM} = 2t\overrightarrow{u_x} + 3t\overrightarrow{u_y} + h\overrightarrow{u_z}$ et $\overrightarrow{v} = 2\overrightarrow{u_x} + 3\overrightarrow{u_y}$.
La norme du vecteur vitesse est : $v = \sqrt{v^2_x+v^2_y+v^2_z}$.
III. Vecteur accélération : $\overrightarrow{a}$
C’est la dérivée de la vitesse par rapport au temps. C’est aussi la dérivée de la dérivée de la position : $\overrightarrow{a} = \dfrac{d\overrightarrow{v}}{dt} = \dfrac{d}{dt} (\dfrac{d\overrightarrow{OM}}{dt}) = \dfrac{d^2\overrightarrow{OM}}{dt^2}$.
On a donc dérivé deux fois la position.
$\overrightarrow{a} = \dfrac{dvx}{dt}\overrightarrow{u_x} + \dfrac{dvy}{dt}\overrightarrow{u_y} + \dfrac{dvz}{dt}\overrightarrow{u_z}$.
Les dérivées correspondent au vecteur accélération en $x, y$ et $z. $
$\overrightarrow{a} = \dfrac{d^2x}{dt^2}\overrightarrow{u_x} + \dfrac{d^2y}{dt^2}\overrightarrow{u_y} +\dfrac{d^2z}{dt^2}\overrightarrow{u_z}$.
Dans les exercices, on donnera $x, y$ et $z.$
Par exemple, si $\overrightarrow{v} = 30\overrightarrow{u_x}$ (on peut l’écrire aussi avec la barre). On dérive la vitesse pour avoir l’accélération : $\overrightarrow{a} = \overrightarrow{0} (m/s^2)$. Si on travaille avec l’écriture en barre, on aura zéro à chaque étage. Pour retrouver l’unité de l’accélération, on sait que c’est la dérivée de la vitesse en m/s sur un temps (s) donc l’accélération est en $m/s^2$ ou $m.s^{-2}$.
Repère de Frenet, mouvement circulaire
I. Repère de Frenet
Soit $M$ un point se déplaçant le long d’une trajectoire. Le repère de Frenet, comme tous les repères, est utile pour décrire position, vitesse et accélération du point $M.$
Le repère cartésien est lié à une origine à un endroit donné puis on va repérer un point $M$ qui se déplace grâce à deux vecteurs unitaires $\overrightarrow{u_x}$, $\overrightarrow{u_y}$ si l’on ne considère que deux dimensions.
Ici, on a deux vecteurs unitaires $\overrightarrow{\tau}$ (vecteur tangent) et $\overrightarrow{n}$ (vecteur normal). Leur particularité est qu’ils vont être associés au point $M$ et qu’ils vont suivre ce point $M.$
Cela va permettre dans certaines situations de décrire beaucoup plus simplement le mouvement :
– Le vecteur $\overrightarrow{\tau}$ est un vecteur unitaire tangent à la trajectoire, c’est-à-dire qu’il est colinéaire au vecteur vitesse $\overrightarrow{v}$, qui est lui-même tangent à la trajectoire. $\overrightarrow{\tau}$ est selon cette tangente dans le même sens que le vecteur vitesse.
– Le vecteur $\overrightarrow{n}$ est quant à lui perpendiculaire au vecteur $\overrightarrow{\tau}$.
$\overrightarrow{\tau}$ et $\overrightarrow{n}$ sont unitaires, ce qui signifie que la norme, l’intensité de chaque vecteur vaut 1. Le repère de Frenet est plus simple à utiliser dans certains cas car le vecteur vitesse peut s’écrire selon le vecteur unitaire $\tau$, à savoir :
$\overrightarrow{v(M)} = v(M)\times \overrightarrow{\tau}$
avec $v(M)$ la valeur de la vitesse.
On rappelle que dans un repère cartésien, on exprime la vitesse ainsi :
$\overrightarrow{v}(M) = x.\overrightarrow{u_x} + y.\overrightarrow{u_y}$
II. Cas du mouvement circulaire
Soit $M$ un point tournant autour de $O$ (l’origine du repère). De nombreux exemples peuvent illustrer ce mouvement circulaire, la Terre autour du Soleil ou la Lune autour du Soleil. On a donc $M$ qui tourne autour d’un centre, $R$ représente le rayon du cercle.
On pose une première hypothèse que $M$ tourne à vitesse constante. Le but est d’arriver à la fin à une relation entre vitesse et vitesse angulaire. Comme $M$ tourne à vitesse constante, on peut écrire :
$v = \dfrac{d}{\Delta t} = \frac{2\pi R}{T}$
On choisit ici la distance et la durée pour faire un tour. $T$ représente la période de révolution. $2\pi R$ est le périmètre du cercle. On calcule ensuite $\omega$ qui est la vitesse angulaire, en radians par seconde ($rad.s^{-1}$).
Pour calculer la vitesse angulaire, on écrit : $\omega = \dfrac{\sigma}{\Delta t} = \dfrac{2 \pi}{T}$
On se base aussi sur la valeur de l’angle et la durée pour effectuer un tour.
On constate donc que $v = \dfrac{2\pi R}{T} = \omega \times R$.
$v$ est en $m.s^{-1}$, $\omega$ en $rad.s^{-1}$ et $R$ en $m$. On peut réécrire le vecteur vitesse $v$ comme étant :
$v = R \times \omega \times t$
Pour rappel, $2\pi = 360°$.
Pour utiliser la deuxième loi de Newton, il peut être intéressant d’écrire le vecteur accélération. L’accélération se décompose en deux termes : l’accélération tangentielle et l’accélération normale. On a ainsi :
$\overrightarrow{a} = \dfrac{dv}{dt} = \dfrac{dv}{dt} \times \overrightarrow{\tau} + \dfrac{v^2}{R} \times \overrightarrow{n}$
Exemple
On considère un manège de rayon $R = 3m$, soit un point $M$ sur le bord entraîné par une vitesse $v = 30 km.h^{-1}$, que vaut son accélération normale ?
On a ainsi : $a_n = \dfrac{v^{2}}{R} \times n$ soit $a_n = \dfrac{v^{2}}{R} = \dfrac{(\dfrac{30}{3,6})^{2}}{3} = 23 m.s^{-2}$
Attention la vitesse est en $km.h^{-1}$.
Remarque : ici la vitesse est constante. Or, la dérivée d’une constante est égale à zéro. Si le manège est à vitesse constante, alors la valeur de $a_t$ est nulle. Finalement, en mouvement accéléré uniforme, $a = a_n$.