Discriminant, solutions
Discriminant, solutions
Discriminant, solutions
Un polynôme du second degré s’écrit $ax^2 + bx + c$, avec $a \neq 0, b, c \in \mathbb{R}$.
Un outil interessant pour l‘étude des racines d’un polynôme du second degré est le discriminant $\Delta$, défini par $\Delta = b^2 – 4ac$.
Il faudra faire attention aux signes (si par exemple $b = -3,$ alors $ b^2 = (-3)^2 = 9$) : on pourra alors utiliser des parenthèses pour se prémunir d’erreurs de calculs.
Le nombre de racines dépend du signe du discriminant. Il existe 6 cas différents selon le signe de $a$ et celui de $\Delta$.
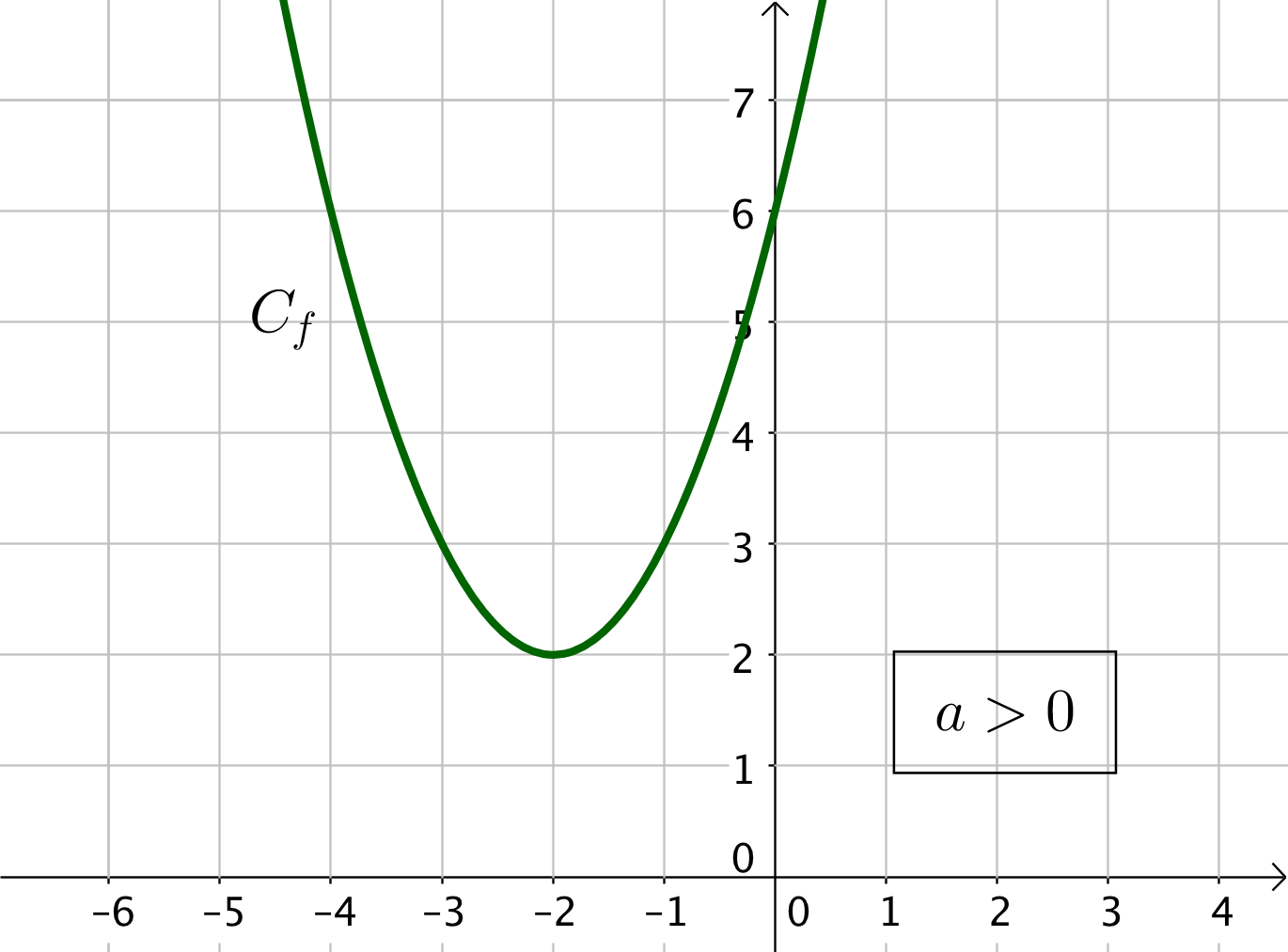
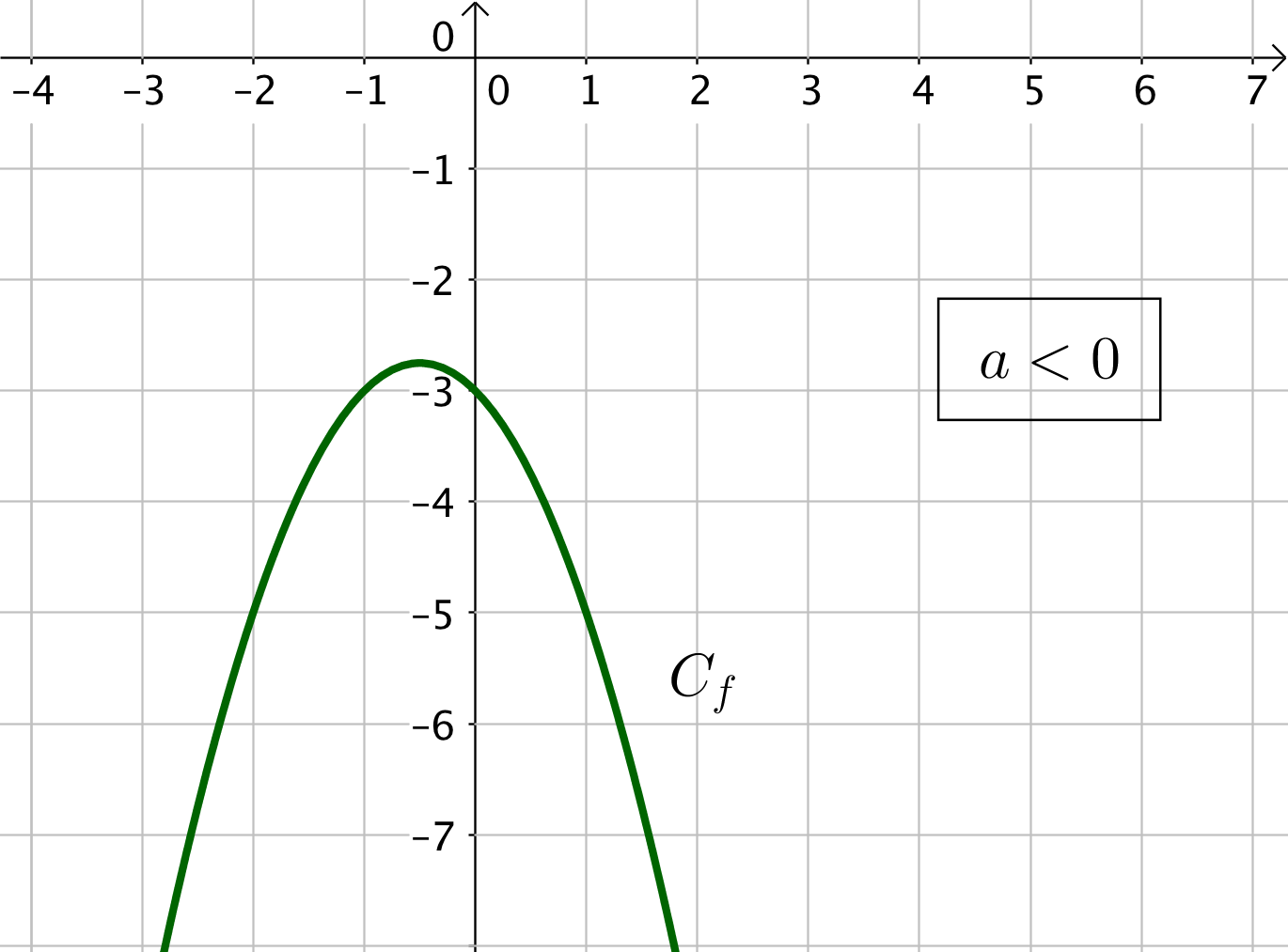
1) Si $\Delta < 0$, la parabole est tournée vers le haut (car $a > 0$) ou vers le bas (si $a < 0$) et il n’y a pas de racine (car $\Delta < 0$).
 |
 |
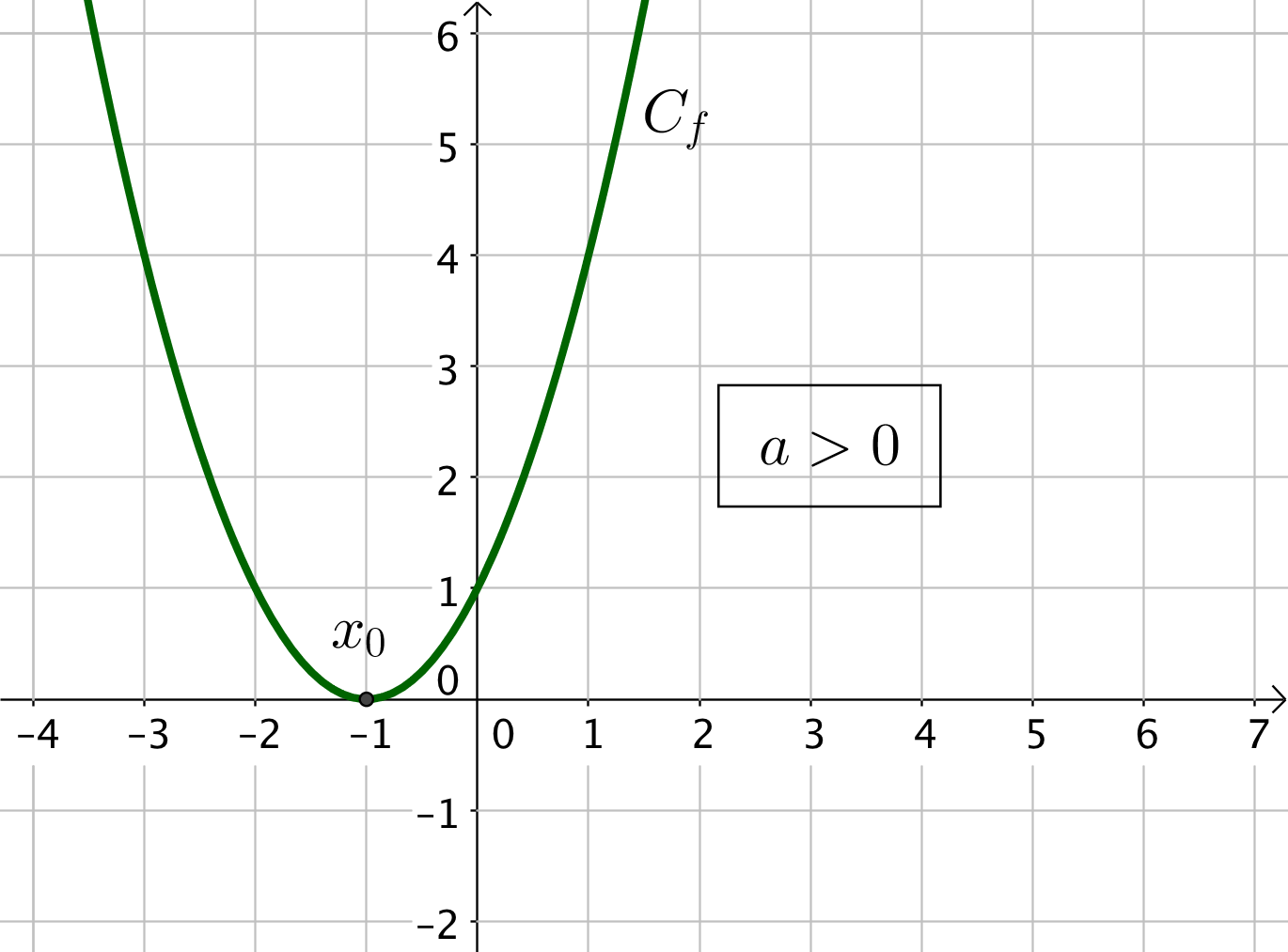
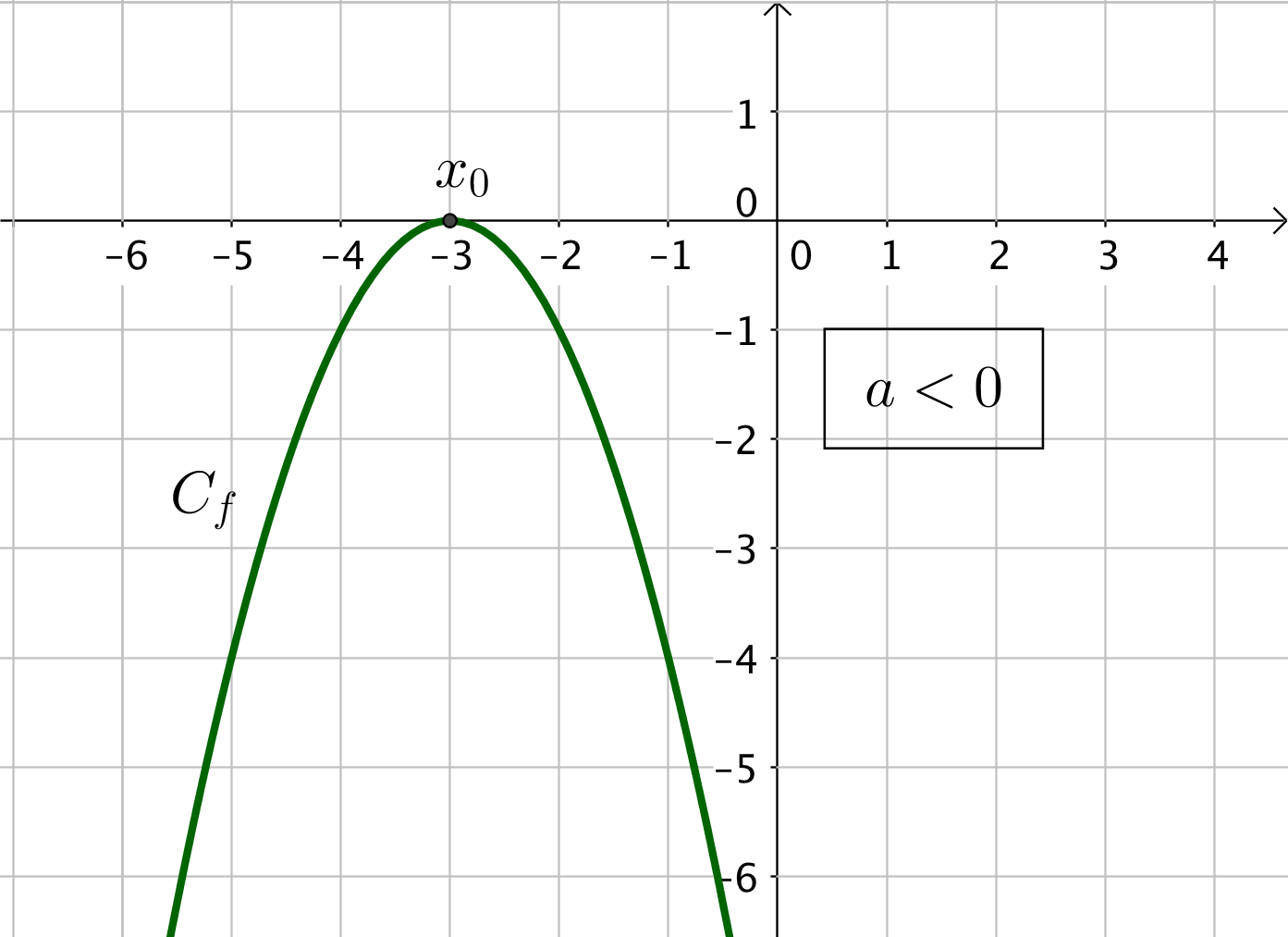
2) Si $\Delta = 0$, l’équation $f(x) = 0$ admet une unique solution : $f$ possède une seule racine $x_0 = \dfrac{-b}{2a}$. La parabole touche l’axe des abscisses en un seul point.
 |
 |
3) Si $\Delta > 0$, l’équation $f(x) = 0$ admet deux solutions : $f$ possède deux racines $x_1 = \dfrac{-b – \sqrt{\Delta}}{2a}$ et $x_1 = \dfrac{-b + \sqrt{\Delta}}{2a}$
 |
 |
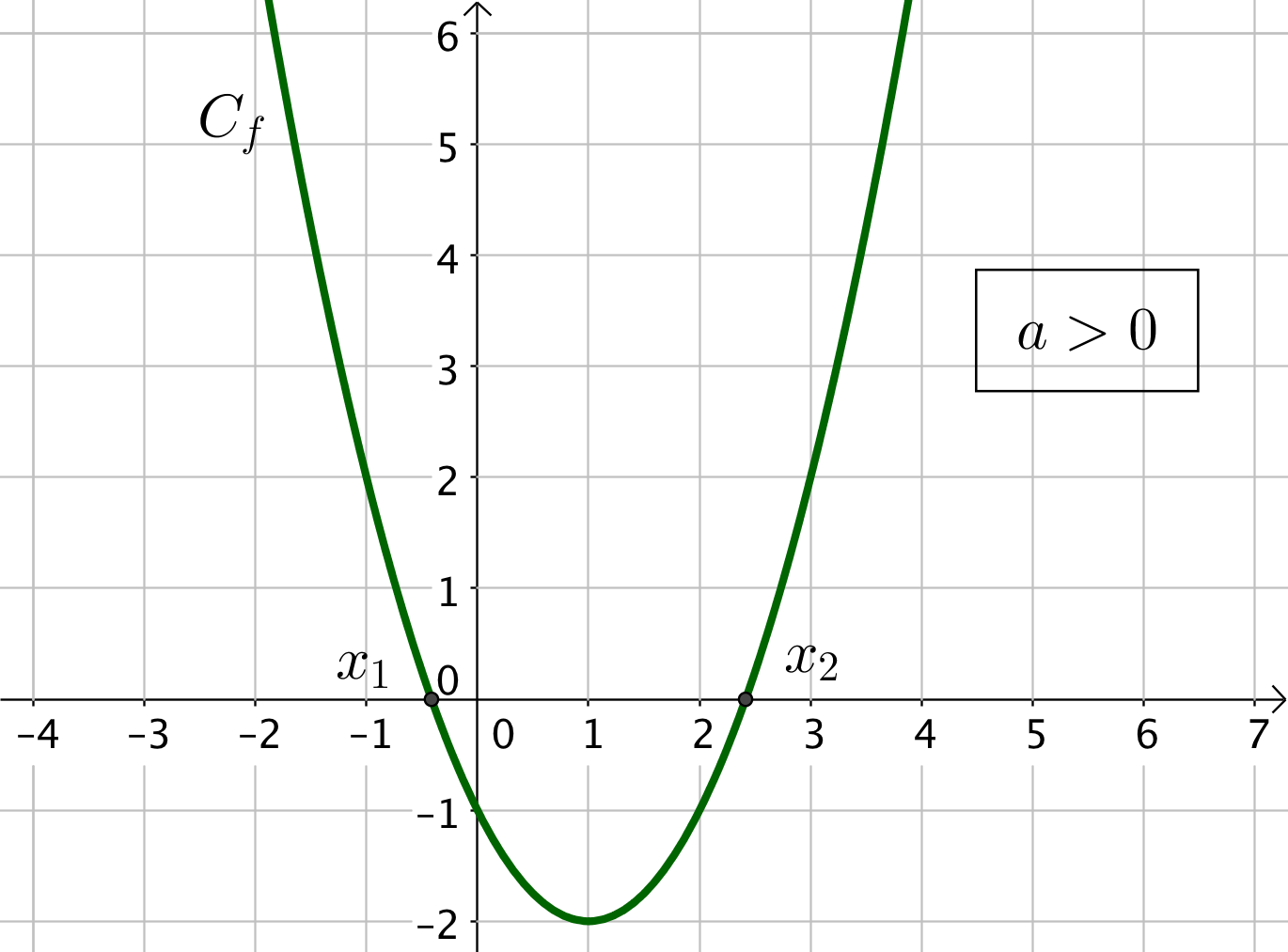
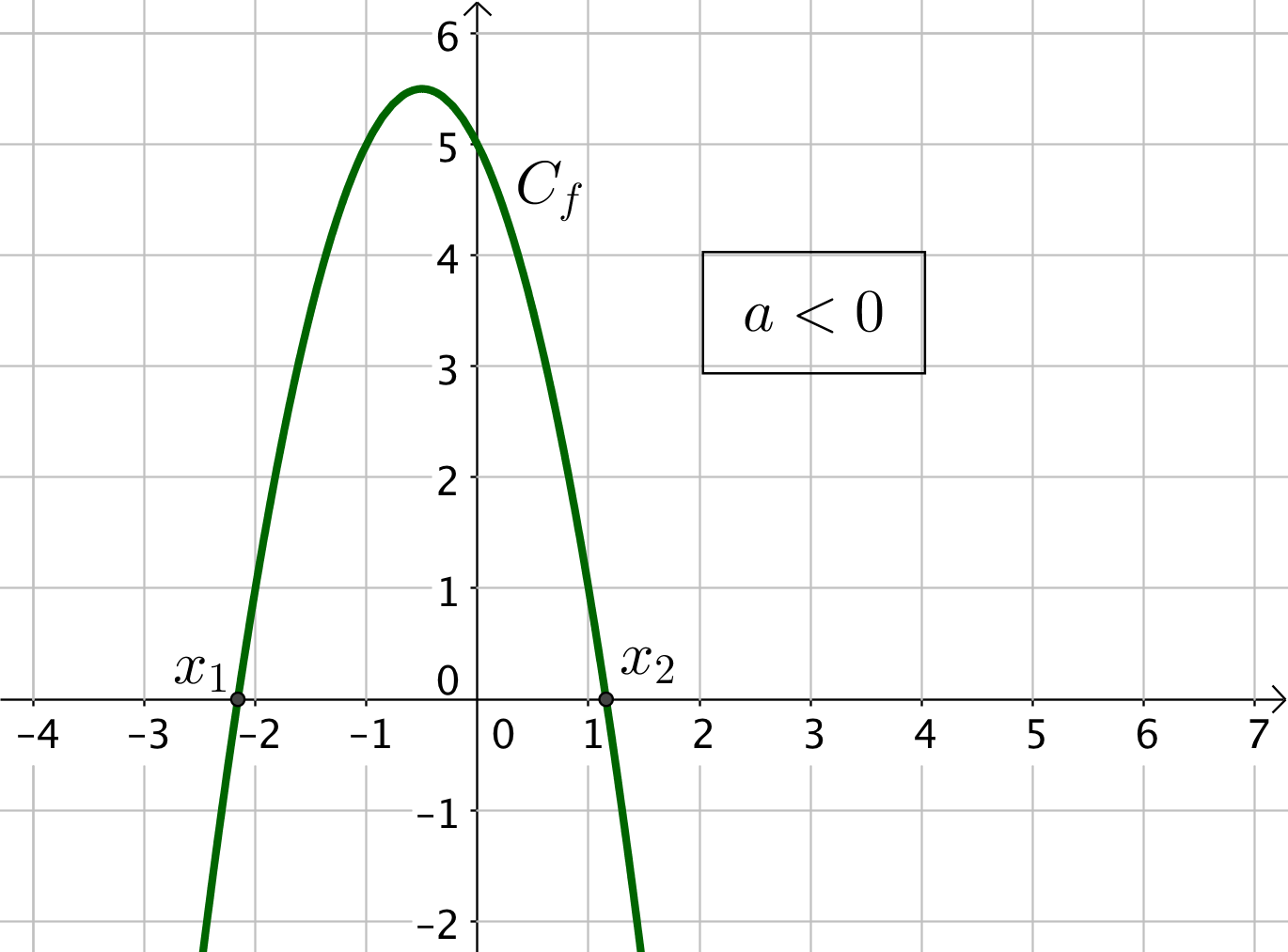