Parallèles et perpendiculaires
Parallèles et perpendiculaires
Droites parallèles, perpendiculaires
Définitions :
Droites sécantes :
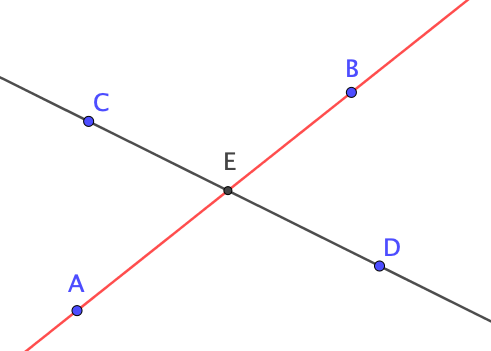
Deux droites qui n’ont qu’un seul point en commun sont des droites sécantes. Ce point commun s’appelle le point d’intersection des deux droites.
Ici, les droites $(AB)$ et $(CD)$ sont sécantes et se coupent en $E$.
Droites perpendiculaires:
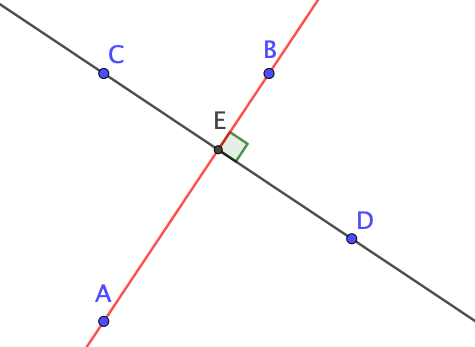
Deux droites sécantes qui forment quatre angles droits sont des droites perpendiculaires. Le symbole $\perp$ signifie « est perpendiculaire à »
On notera ici : $(AB)\perp(CD)$
Droites parallèles:
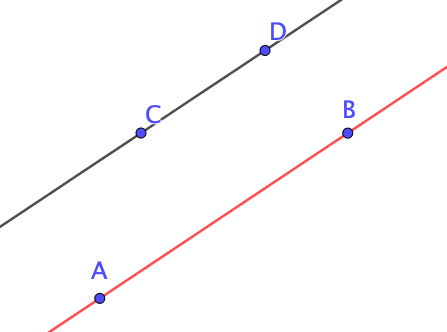
Deux droites qui ne sont pas sécantes sont des droites parallèles. Elles n’ont aucun point commun. Le symbole $//$ signifie « est parallèle à »
On notera ici : $(AB) // (CD)$
Commentaire :
Cette géométrie élémentaire a été énoncée clairement par Euclide, un mathématicien de la Grèce Antique (environ 300 av JC).
La géométrie étudiée ici est la géométrie euclidienne.
La médiatrice d'un segment
Médiatrice d’un segment
Définition
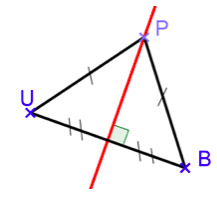
La médiatrice d’un segment est la droite perpendiculaire à ce segment en son milieu.
G est le milieu du segment [AB] et $d \perp (AB)$ donc d est la médiatrice du segment [AB].
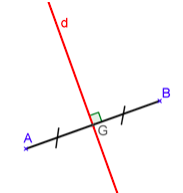
Propriété de la médiatrice :
La médiatrice d’un segment est l’ensemble des points du plan équidistants des extrémités de ce segment.
Remarque : équidistant signifie « à égale distance ».
On a en fait deux propriétés :
Si un point P appartient à la médiatrice du segment [UB] alors PU=PB (c’est-à-dire P est équidistant des extrémités du segment [UB]).
Si un point P est équidistant des extrémités d’un segment [UB] (c’est-à-dire si PU=PB) alors P appartient à la médiatrice de [UB].
Commentaires
-Grâce à ces propriétés nous avons une construction au compas.
-Cela signifie aussi que tous les points qui n’appartiennent pas à la médiatrice d’un segment ne sont pas équidistants des extrémités de ce segment. Ils sont donc plus proches de l’une des deux extrémités que de l’autre.
Le petit plus des Bons Profs
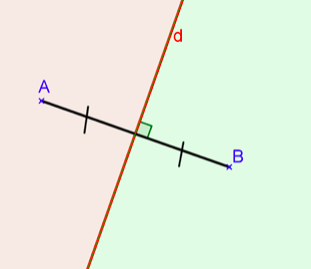
On a ainsi un partage du plan en trois parties : les points de la médiatrice du segment, les points du demi-plan rose et ceux du demi-plan vert ci-dessous
En rose, un demi-plan : les points plus proches du point A ; En vert, un demi-plan : les points plus proches du point B
