Echantillonnage
Echantillonnage
On se demande si à partir d’une population assez grande, on peut étudier un caractère dont on connait la proportion $p$.
On considère pour se faire un échantillon de taille $n$ connue et on cherche à déterminer si cet échantillon représente la population initiale pour le caractère étudié au seuil de 95% de confiance.
Le nombre d’individus présentant le caractère étudié au sein de la population suit une loi binomiale de paramètres $n$ et $p$.
La variable aléatoire associée est notée $X$.
On cherche alors le plus petit entier $a$ tel que $P(X \leq a ) > 0,025$.
De même on cherche le plus petit entier $b$ tel que $P(X \leq b ) \geq 0,975$.
L’intervalle de fluctuation vaut $I_f = \left [ \dfrac{a}{n}; \dfrac{b}{n} \right ]$.
A l’issue de ce calcul, il faut prendre une décision, c’est à dire confirmer ou infirmer que l’échantillon correspond à la population.
Pour cela, on suppose que l’échantillon représente la population : c’est une hypothèse.
Si la fréquence $f$ constatée appartient à $I_f$ alors on accepte l’hypothèse : l’échantillon représente la population.
Sinon, on refuse l’hypothèse.
Exemple :
On considère que 45% de la population française possède des lunettes.
On étudie un échantillon de 35 personnes : on définit alors la variable aléatoire $X$ qui suit la loi binomiale de paramètres $n = 35$ et $p = 0,45$.
A partir de la calculatrice, on obtient le tableau suivant :
Par lecture dans le tableau, on voit que $A = 10$ et $b = 22$.
Ainsi, $I_f = \left [ \dfrac{10}{35}; \dfrac{22}{35} \right ]$ au seuil de 95%.
Prise de décision :
Si parmi cet échantillon 17 personnes ont des lunettes, la fréquence du caractère est donc $f = \dfrac{17}{35}$.
Ainsi $f \in I_f$ : cet échantillon représente donc bien la population.
Intervalle de fluctuation
Intervalle de fluctuation (Loi Binomiale)
Définition :
Si $X$ suit une loi binomiale de paramètres $n$ et $p$ vérifiants les trois conditions suivantes :
$\left \{ \begin{array}{l} 0,2 < p < 0,8 \\ n \geq 25 \\ np \geq 5 \end{array} \right. $,
alors l’intervalle de fluctuation au seuil de 95% de la fréquence $f = \dfrac{X}{n}$ sur un échantillon de taille $n$ est :
$I = \left [ \dfrac{a}{n}; \dfrac{b}{n} \right ]$ où $a$ et $b$ sont deux entiers naturels les plus petits possibles tels que : $\left \{ \begin{array}{l} P(X \leq a) > 0,025 \\ P(X \leq b) \geq 0,975 \end{array} \right.$
Exemple :On considère un jeu de trente deux cartes.
On s’intéresse à l’événement $A = \text{“Tirer un coeur”}$ dont la probabilité est $p = 0,25$ : il s’agit d’une expérience de Bernoulli de paramètre $p = 0,25$.
On effectue 90 tirages avec remise indépendants les uns des autres : c’est donc un schéma de Bernoulli et on définit ainsi une loi binomiale de paramètres $n = 90$ et $p = 0,25$.
Lors d’un tirage, on obtient 34 coeurs. Peut-on supposer que le jeu est truqué ?
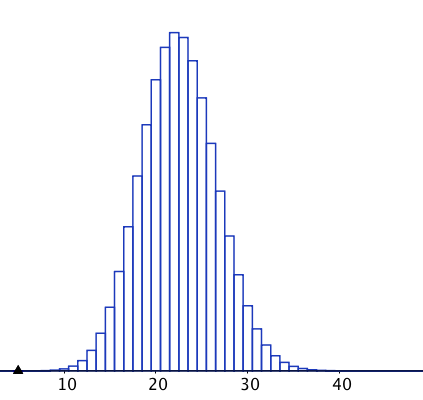
On définit donc la variable aléatoire $X$ qui suit la loi binomiale de paramètres $n = 90$ et $p = 0,25$ dont la représentation graphique est la suivante :
On doit vérifier que les conditions portant sur $n$ et $p$ sont vérifiées afin d’utiliser l’intervalle de fluctuation :
$0,2 < p < 0,8$; $n = 90 \geq 25$; $np = 22,5 \geq 5$.
Il faut donc chercher les deux réels $a$ et $b$ qui sont les plus petits possibles tels que :
$\left \{ \begin{array}{l} P(X \leq a) > 0,025 \\ P(X \leq b) \geq 0,975 \end{array} \right.$
Pour se faire, on calcule le tableau des fréquences cumulées. En voici un extrait (entre 10 et 17 succès)
Ce tableau contient dans une première ligne le nombre du succès, dans une seconde la probabilité associée, et dans la troisième les probabilités cumulées.
On cherche donc le premier entier pour lequel la probabilité cumulée dépasse 0,025 : on trouve $a = 15$.
On cherche de même le premier entier pour lequel la probabilité cumulée dépasse 0,975 : on trouve $b = 31$.
Ainsi, $I = \left [ \dfrac{15}{90}; \dfrac{31}{90} \right ] \approx [0,1667; 0,3444]$.
On a tiré 34 coeurs : la fréquence observée est donc égale à $\dfrac{34}{90} \approx 0,3778$.
Or dans 95% des cas, la fréquence observée devrait appartenir à $I$ ce qui n’est pas le cas ici.
Ainsi, on peut affirmer avec 5% d’erreur que le jeu est truqué.