Effet joule

Effet Joule

Effet Joule

I. Puissance et énergie électrique

Lien puissance/énergie

La puissance représente l’énergie par unité de temps.

$P = \dfrac{E}{Δt}$

Avec $P$ en watt (W), $E$ en joule (J) et $t$ en seconde (s).

Expression de la puissance électrique

On distingue deux cas selon si le dipôle est récepteur (lampe, moteur, résistance électrique) ou générateur (pile, source de tension ou de courant). En convention récepteur, l’intensité électrique $I$ et la tension $U$ sont de sens opposés contrairement à la convention générateur où les deux sont dans le même sens. On a alors :

$P_{reçue} = U \times I$ en convention récepteur.

$P_{fournie} = U \times I$ en convention générateur.

ATTENTION : l’expression est la même sauf que dans un cas le récepteur prend de l’énergie du circuit $(P_{reçue}> 0)$ tandis que le générateur donne de l’énergie $(P_{fournie}> 0).$

II. Effet Joule

Qu’est-ce que l’effet Joule ?

Vision microscopique

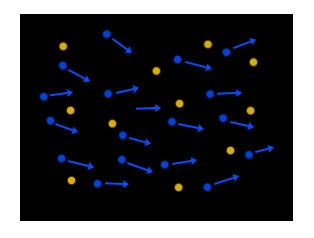
Les cations (en jaune) sont fixes tandis que les électrons (en bleu) sont mobiles. Les flèches représentent les vitesses des électrons. La direction pour chaque électron est aléatoire même si on distingue quand même une tendance des électrons à aller de la gauche vers la droite. Le mouvement des électrons s’effectue dans un ensemble de cations. L’électron va s’approcher d’un cation et le frotter, ce qui provoque une diminution de l’énergie mécanique et la création d’énergie thermique.

L’effet Joule est donc le fait que les électrons s’approchent trop souvent des cations. Ces électrons vont donc céder leur énergie mécanique et la transférer en énergie thermique.

Effet Joule : définition

Dans un conducteur ohmique de résistance $R,$ l’énergie électrique reçue par la résistance est convertie en énergie thermique. L’énergie électrique entre donc dans la résistance et en sortie on obtient de l’énergie thermique.

Puissance dissipée par effet Joule

Comment exprimer la puissance dissipée par effet Joule ?

La puissance dissipée par effet Joule est la puissance reçue par la résistance ou conducteur ohmique. On sait que $P_{reçue} = U \times I$ et que la loi d’Ohm nous permet d’écrire $U = R \times I.$

On peut donc exprimer la puissance dissipée par effet Joule de deux manières :

$P_{joule} =P_{reçue}= R \times I^2$

OU

$P_{joule} =P_{reçue} = \dfrac{U^2}{R}$