La sphère
La sphère
La sphère
Définition
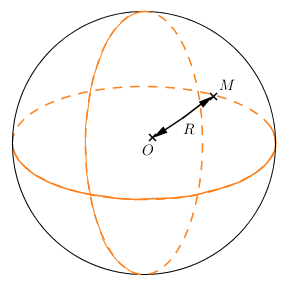
Une sphère de centre $O$ et de rayon $R$ est l’ensemble de tous les points $M$ de l’espace situés à la distance $R$ du point $O$.
On a donc $OM=R$.
Son équation cartésienne est : $(x-x_O)^2+(y-y_O)^2+(z-z_O)^2=R^2$.
Exemple
Ecrire l’équation cartésienne de sphère de centre $\Omega$ et de rayon 3 notée $S(\Omega;3)$ avec $\Omega(2;0;-1)$
Son équation cartésienne est
S: $(x-2)^2+(y-0)^2+(z-(-1))^2 = 3^2$.
En développant, on obtient :
S: $x^2-4x +4+y^2+z^2+2z+1 = 9$.
S: $x^2+y^2+z^2-4x+2z = 4$