Équations de droites - Définition
Équations de droites
Définition:
On se place dans le plan muni d’un repère.
Toute droite du plan possède une équation de la forme :
$x = k$ si il s’agit d’une droite parallèle à $(Oy)$, où $k$ est un réel
$y = ax + b$ si il s’agit d’une droite sécante à $(Oy)$ : c’est l’équation réduite de la droite.
$a$ est un réel correspondant au coefficient directeur de la droite, il donne l’inclinaison de la droite.
$b$ est un réel correspondant à l’ordonnée à l’origine, c’est à dire l’ordonnée du point d’intersection de la droite avec l’axe des ordonnées.
Exemple :
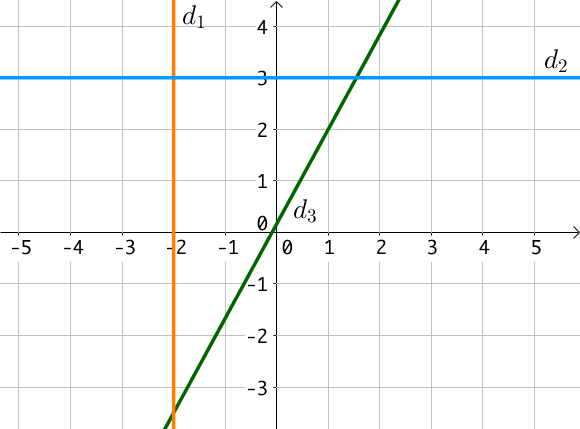
La droite $(d_1)$ est parallèle à l’axe des ordonnées. Son équation est donc de la forme $x = k$. Ainsi $k$ correspond à la valeur de l’abscisse. Tous les points de la droite ont même abscisse : $-2$, alors que leurs ordonnées sont variables. Ainsi, $x = -2$.
Un point quelconque appartenant à la droite $(d_2)$ a pour ordonnée 3, et une abscisse quelconque : l’équation réduite de cette droite est donc $y = 3$. Il s’agit d’une équation réduite car on peut écrire cette équation comme $y = 0\times x + 3$.
La droite $(d_3)$ a une équation de la forme $y = ax + b$ mais il n’est pas possible de déterminer $a$ et $b$ car on ne dispose d’aucune donnée pour cette droite. Il faudrait au moins les coordonnées de deux points.
Droites parallèles
Considérons deux droites $(\Delta)$ et $(\Delta ‘)$ d’équations réduites :
$\Delta : y = ax+b$
$\Delta’ : y = a’x+b’$
Les droites $(\Delta)$ et $(\Delta ‘)$ sont parallèles si et seulement si elles ont le même coefficient directeur,
Autrement dit $(\Delta) // (\Delta ‘) \iff a =a’$
Si les deux droites ont une équation de la forme
$\Delta : x = k$
$\Delta’ : x = k’$
alors elles sont parallèles.
Points alignés
Points alignés
Deux points étant toujours alignés, on considérera trois points ou plus dans la suite.
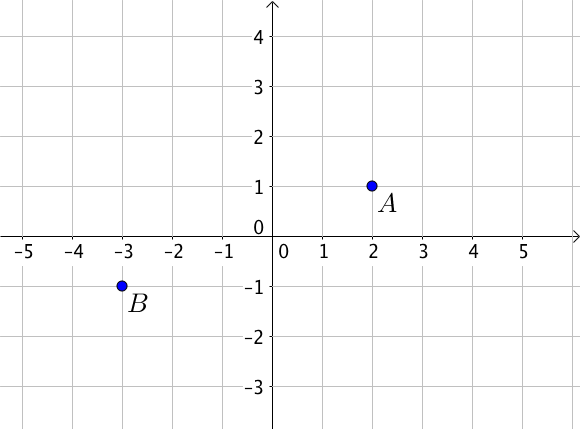
Soient trois points $A(2;1), B(-3; -1)$ et $C(12; 5)$,
On se contente de représenter uniquement les points $A$ et $B$.
Les points $A, B$ et $C$ sont ils alignés ?
Méthode :
Pour répondre à cette question, la méthode consiste à calculer le coefficient directeur de la droite $(AB)$ puis le coefficient de la droite $(AC)$.
Or si ces coefficients directeurs sont égaux, alors les deux droites sont parallèles.
Mais ces deux droites possèdent alors un point commun : $A$, les deux droites sont donc confondues : les points sont donc alignés.
Il faut donc commencer par calculer les deux coefficients directeurs.
Le coefficient directeur de la droite $(AB)$ est :
$a =\dfrac{y_B-Y_A}{x_B-x_A}=\dfrac{-1 -1}{-3 – 2} = \dfrac{2}{5}$.
Le coefficient directeur de la droite $(AC)$ est :
$a’ =\dfrac{y_C-Y_A}{x_C-x_A}= \dfrac{5 -1}{12 – 2} = \dfrac{4}{10} = \dfrac{2}{5}$.
Ainsi $a = a’$, les droites $(AB)$ et $(AC)$ sont donc parallèles et ont un point commun : les points $A, B$ et $C$ sont alignés.
Le fait de tracer une droite reliant les trois points ne prouve pas l’alignement.