Équations différentielles y’ = ay , avec a réel
Équations différentielles $y’ = ay$ avec $a \in \mathbb{R}$
Propriété
Les solutions de l’équation différentielle $y’ = ay$ avec $a \in \mathbb{R}$ sont les fonctions de la forme $x \mapsto Ce^{ax}$ où $C$ est une constante réelle.
Démonstration
On commence par démontrer que toute fonction de la forme $x \mapsto Ce^{ax}$ où $C$ est une constante réelle est solution de l’équation différentielle $y’ = ay$.
Soit $f$ la fonction définie sur $\mathbb{R}$ par
$f(x) = Ce^{ax}$.
$f$ est dérivable sur $\mathbb{R}$ en tant que composée de deux fonctions dérivables sur $\mathbb{R}$.
On pose $u(x) = ax$. Ainsi,
$f(x) = Ce^{u(x)}$.
On sait en outre que $\left ( e^u \right )’ = u’e^u$ pour toute fonction $u$.
Ainsi, $f'(x) = C \times ae^{ax}$, car la dérivée de $u(x) = ax$ est $u'(x) = a$.
Finalement,
$f'(x) = a \times Ce^{ax} = a \times f(x)$.
On vient donc de montrer que $f$ est solution de l’équation différentielle $y’ = ay$.
La deuxième partie de la démonstration consiste à montrer que toute solution de l’équation différentielle $y’ = ay$ s’écrit sous la forme $x \mapsto Ce^{ax}$.
On propose pour cette seconde partie deux démonstrations et on laissera au lecteur le soin de choisir celle qu’il préfèrera.
Première démonstration possible
Soit $f$ une fonction non nulle, solution de l’équation différentielle $y’ = ay$ (si $f$ est nulle, $f$ est de la forme attendu en prenant $C = 0$),
alors $f'(x) = a f(x)$ que l’on réécrit $\dfrac{f'(x)}{f(x)} = a$.
On intègre alors cette relation.
Une primitive de $a$ est $ax + b$ où $b$ est une constante.
Une primitive de $\dfrac{f'(x)}{f(x)}$ est $\ln \left | f(x) \right |$.
L’équation se réécrit alors
$\ln \left | f(x) \right | = ax + b$.
En appliquant à cette nouvelle équation la fonction exponentielle on obtient l’égalité suivante :
$|f(x)| = e^{ax+b}= e^b \times e^{ax}$.
Comme l’exponentielle est toujours positive, on peut écrire :
$f(x) = \pm e^b \times e^{ax}$.
En posant $C = \pm e^b$ on a alors
$f(x) = Ce^{ax}$, c’est ce que l’on voulait démontrer.
Deuxième démonstration possible
Soit $f$ une fonction solution de l’équation $y’ = ay$.
On pose pour tout $x \in \mathbb{R} \;h(x) = e^{-ax}f(x)$.
$h$ est dérivable sur $\mathbb{R}$ en tant que produit de fonctions dérivables sur $\mathbb{R}$.
Ainsi, soit $x \in \mathbb{R}$,
$h'(x) = -ae^{-ax}f(x) + e^{ax}f'(x)$.
Or comme $f$ est solution de l’équation différentielle $y’ = ay$ on a $f'(x) = af(x)$.
Ainsi, $h'(x) = -ae^{-ax}f(x) + e^{ax}(af(x)) =0$.
Ainsi il existe $C \in \mathbb{R}$ telle que $h(x) = C$.
Finalement, $e^{-ax}f(x) = C$ c’est à dire $f(x) = Ce^{ax}$, c’est à dire ce que l’on souhaitait démontrer.
Exercice type
On considère l’équation différentielle $2y’ – 3y = 0$.
1) Déterminer la forme générale des solutions de l’équation
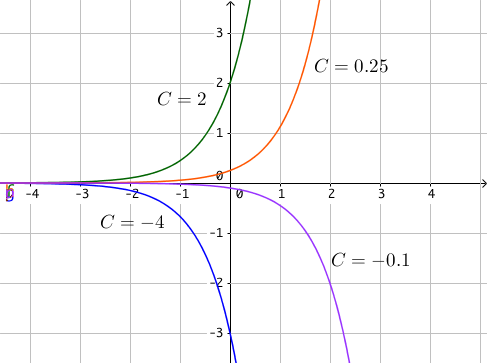
2) Représenter à l’aide de la calculatrice quelques courbes des fonctions solutions
3) Déterminer l’unique solution $f$ telle que $f(1) = 2$
Correction
1) La première étape consiste à se ramener à une équation de la forme $y’ = ay$ avec $a$ un réel que l’on déterminera.
$2y’ – 3y = 0 \iff 2y’ = 3y \iff y’ = \dfrac{3}{2}y$.
Ainsi, $a = \dfrac{3}{2}$ et les solutions sont de la forme $y(x) = Ce^{\frac{3}{2}x}$ avec $C$ une constante réelle.
2) On donne ici quelques courbes de différentes fonctions solutions pour lesquelles on a choisit des valeurs quelconques de $C$.
3) On cherche dans cette question la solution particulière vérifiant $f(1) = 2$.
Comme $f$ est solution de l’équation différentielle, elle est de la forme
$f(x) = Ce^{\frac{3}{2}x}$ avec $C$ une constante réelle que l’on va déterminer.
En effet,
$f(1) = 2 \iff Ce^{\frac{3}{2}\times 1} = 2 \iff C = 2 e^{-\frac{3}{2}}$.
Finalement, en remplaçant dans l’expression
$f(x) = 2 e^{-\frac{3}{2}} \times e^{\frac{3}{2}x}$
En conclusion, on a :
$f(x) = 2 e^{\frac{3}{2} (x – 1)}$.