Échantilloner des populations
Échantilloner des populations
Il existe plusieurs techniques pour pouvoir échantillonner des populations.
I. Méthode de capture-relargage-recapture
L’une d’elle est la méthode de capture-relargage-recapture.
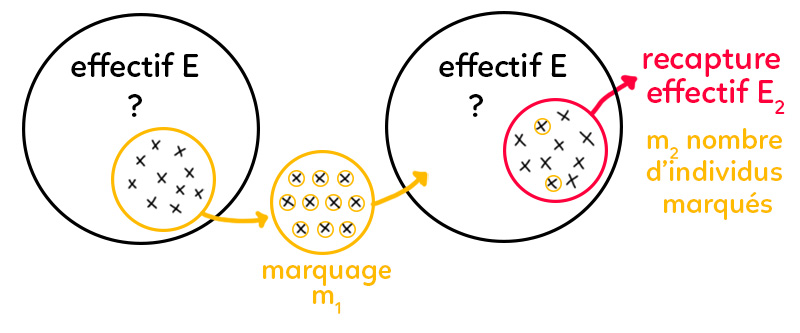
Prenons un effectif d’une population, $E,$ qui nous est inconnu, et on aimerait savoir de combien d’individus est constituée cette population. On va prélever, donc capturer, un certain nombre d’individus, et on va les marquer. C’est pourquoi on a ici marqué marquage $m_1.$ Ici on marque $10$ individus prélevés dans cet effectif. Le marquage ça peut par exemple être le baguage d’oiseaux, faire des encoches sur des carapaces de tortues ou toute technique qui va permettre de reconnaître les individus une fois qu’ils auront été recapturés. En effet, ces individus marqués $m_1$ vont être relâchés dans leur environnement. Ils vont donc se mélanger aux autres individus de leur population.
On va alors effectuer après ce relargage une recapture. On va re-prélever un effectif $E_2$ de $10$ individus, et on va regarder sur ces individus combien on a d’individus marqués, qu’on a appelés $m_2.$ Dans cet exemple on en a $2.$
Quand on suppose qu’il y a une proportionnalité entre le nombre d’individus secondairement marqués avec l’effectif prélevé par rapport à l’effectif initial, on peut donc dire que :
$dfrac{m_1}{E}= dfrac{m_2}{E_2}$
On déduit l’effectif par cette quatrième proportionnelle.
On a $E = dfrac{m_1 times E_2}{m_2}$
Dans notre exemple, $m_1$ est égal à $10$ individus :
On a $E = dfrac{10 times 10}{2}= 50$
L’effectif $E$ de la population est de $50$ individus.
II. Échantillonnages et intervalle de confiance
Une autre technique pour échantillonner les populations est d’utiliser l’intervalle de confiance.
C’est une probabilité que notre effectif se trouve entre deux valeurs mathématiques que l’on peut calculer par la formule :
$[f – dfrac{1}{sqrt{n}} ; f + dfrac{1}{sqrt{n}}]$
Exemple des tortues : chez les tortues le sexe n’est pas déterminé génétiquement comme chez les mammifères, c’est lié à la température d’incubation. Plusieurs espèces ont le sexe qui est déterminé par la température d’incubation des œufs, c’est le cas également chez les crocodiles, chez les alligators, chez certaines espèces de lézards.
Prenons notre population théorique de tortues. Sur ces tortues, on va en échantillonner $20$ dans le milieu. Sur ces $20$ tortues, on trouve $8$ femelles et $12$ mâles. Admettons que l’on s’intéresse à la proportion de femelles chez cette espèce de tortues. On va appliquer la formule d’intervalle de confiance qui va être qu’au minimum la proportion de torture femelles dans la population correspond à la fréquence des femelles de l’effectif de l’échantillon (on a $8$ femelles sur $20$ tortues, soit $40$ % ou $0,4 -1$ sur l’effectif de notre échantillon, soit $20$ ; et au maximum on aura $0,4 + 1$ sur racine de $20$ pour notre proportion de tortues femelles dans la population.
Si on effectue les calculs, on trouve que le nombre de tortues femelles dans la population est compris entre $18$ et $62$ %. L’écart peut paraître important : c’est normal puisqu’il est déterminé par notre effectif. On ne peut pas avoir un intervalle de confiance de $100$ %. Pour avoir un intervalle de confiance de $100$ %, il faudrait que l’on collecte tous les individus du milieu.
Cette formule permet uniquement de dire qu’entre $18$ % et $62$ % de nos tortues seront des femelles avec un intervalle de confiance de $95$ %. Il n’y a que $5$ % de probabilité pour qu’on se trouve en dehors de cet intervalle.
Si l’on veut rétrécir l’écart de cet intervalle, il faut que l’on prélève davantage de tortues. Plus l’effectif sera grand, plus on pourra affiner cet écart, cet intervalle de confiance. On en vient donc à l’importance de la taille de l’échantillon.
III. L’importance de la taille de l’échantillon
Admettons que l’on vienne dans votre lycée et que l’on souhaite s’intéresser au nombre d’élèves qui portent des lunettes dans ce dernier. Si on examine $10$ élèves, on peut très bien ne trouver aucun élève portant des lunettes sur ces $10$ élèves. Est-ce que cela signifie pour autant que dans votre lycée aucun élève ne porte des lunettes ? Non.
On pourrait très bien avoir, autre cas extrême, $10$ élèves ayant tous des lunettes. Est-ce que cela signifie pour autant que dans votre lycée tous les élèves ont des problèmes de vue ? Absolument pas.
On comprend donc que la taille de l’échantillon va avoir son importance. Plus l’échantillon sera important, plus on sera statistiquement proche des effectifs de la population effective.
Estimer la biodiversité d'un milieu
Estimer la biodiversité d’un milieu
I. État des lieux de la biodiversité
La biodiversité est la diversité des espèces vivant sur notre planète, la Terre.
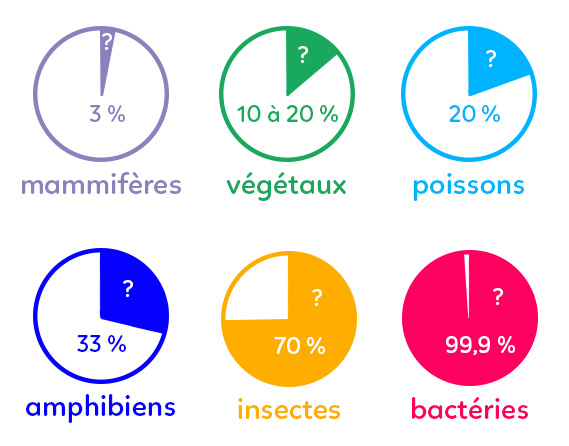
On a dénombré dans la littérature scientifique à peu près 1,5 million d’espèces, donc ce sont des espèces qui ont été décrites. Ceci étant, il en existerait plus de 8 millions sur notre planète. En effet, 3 % des espèces de mammifères nous sont inconnues (ce sont à peu près des estimations par rapport au nombre d’espèces que l’on continue encore de découvrir), 10 à 20 % des végétaux, 20 % des poissons, 33 % des amphibiens. Concernant les insectes, on estime que 70 % des espèces d’insectes nous sont inconnues, et concernant les bactéries, on n’aurait découvert que 0,1 % de toutes les espèces.
II. Les composantes de la biodiversité
On peut estimer la biodiversité à travers ses composantes. Trois termes sont ici à retenir :
– la richesse spécifique : elle correspond au nombre d’espèces différentes présentes dans un milieu.
– l’abondance : elle correspond au nombre d’individus pour chaque espèce.
– l’équitabilité : elle permet de savoir si l’abondance entre chaque espèce dans ce milieu est équilibrée.
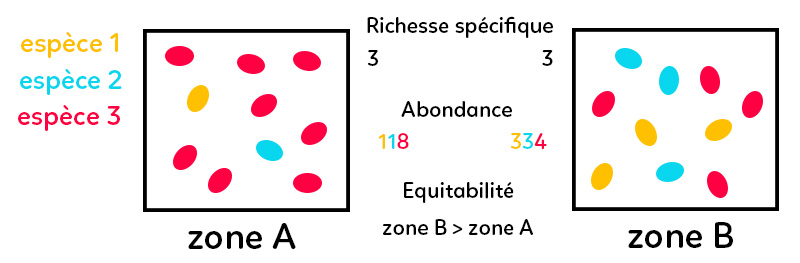
Exemple : nous avons deux zones, une zone A, une zone B qui présentent chacune des espèces matérialisées par ces petits ovales de couleur. Trois espèces : espèce 1, espèce 3 et espèce 3.
On remarque que ces deux zones, zone A, zone B, ont la même richesse spécifique puisque dans les deux carrés qui les représentent, il y a le même nombre de couleurs différentes. En terme d’abondance, dans la zone A, il y a un individu de l’espèce jaune, un individu de l’espèce bleue et huit de l’espèce rouge, alors que dans la zone B, il y a trois jaunes, trois bleus et quatre rouges. Cela signifie que l’équitabilité n’est pas la même : en effet, celle de la zone B est supérieure à celle de la zone A. Il y a en terme d’abondance relative une part plus équitable entre le nombre des différentes espèces dans cette zone que dans l’autre.
Ainsi, il est vraiment important de ne pas estimer la biodiversité uniquement avec sa richesse spécifique, c’est-à-dire avec le nombre d’espèces présentes dans ce milieu. L’abondance et l’équitabilité sont fondamentales.
III. Mesurer la biodiversité
Cette biodiversité, on peut la mesurer. Par exemple, par des techniques d’échantillonnage, que ce soit des spécimens ou de l’ADN.
– Techniques d’échantillonnage de spécimens : on prend par exemple la goélette Tara de l’expédition Tara Océans qui sillonne les océans pour répondre à différentes missions de scientifiques. Ainsi, pendant quelques années elle a par exemple étudié le plancton marin, dont le phytoplancton est assez méconnu. La goélette, sur ces quelques années, a récolté plus de 27 000 échantillons qui nous ont permis de mieux connaître la richesse relative en espèce du phytoplancton, c’est-à-dire le plancton marin responsable de la photosynthèse.
– Techniques d’échantillonnage avec de l’ADN : c’est-ce qu’on appelle l’ADN environnemental, ou la métagénomique. Dans ce cas, on récupère dans un échantillon de sol, d’eau, tous les ADN présents. Cela nous permet de quantifier l’abondance relative d’une espèce, d’entériner aussi la présence d’une espèce, on ne la voit pas mais on a retrouvé son ADN donc on sait qu’elle est là ou qu’elle a été là, et de découvrir, évidemment, de nouvelles espèces.