Fonction Cosinus et Sinus. Parité, périodicité. Dérivées et représentation graphique
Fonctions cosinus et sinus – Parité, périodicité – Dérivées et représentation graphique
I) Fonctions cosinus et sinus
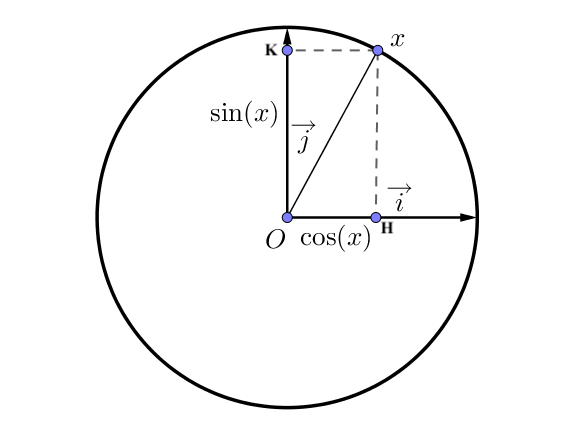
Dans le plan muni d’un repère orthonormé $(O, \overrightarrow{i}, \overrightarrow{j})$ et orienté dans le sens direct (le sens anti-horaire), on considère!re un cercle trigonométrique de centre $O$.
Pour tout réel $x$, considérons le point $N$ de la droite orientée des réels d’abscisse $x$.
A ce point, on fait correspondre un unique point $M$ sur le cercle trigonométrique par enroulement de la droite des réels sur ce cercle.
On appelle $H$ le point d’intersection entre la droite perpendiculaire à l’axe des abscisses passant par $M$ et l’axe des abscisses.
On appelle $K$ le point d’intersection entre la droite perpendiculaire à l’axe des ordonnées passant par $M$ et l’axe des ordonnées.
Définition :
Pour tout nombre réel $x$, on définit :
– la fonction cosinus et on note $x \mapsto \cos(x)$ où $\cos(x)$ correspond à l’abscisse du point $M$, c’est à dire la distance $OH$
– la fonction sinus et on note $x \mapsto \sin(x)$ où $\sin(x)$ correspond à l’ordonnée du point $M$, c’est à dire la distance $OK$
II) Parité – Périodicité
a) Propriétés de parité des fonctions cosinus et sinus
Pour tout nombre réel $x$,
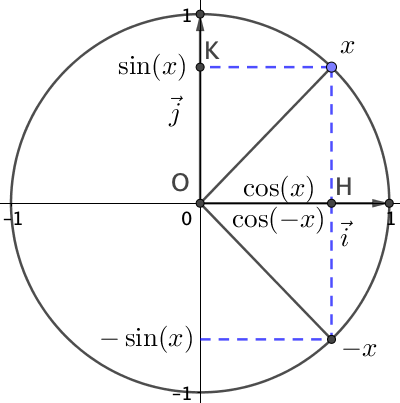
$\cos(-x) = \cos(x)$. On dit que la fonction cosinus est paire.
Dans un repère orthogonal, la courbe représentative de la fonction cosinus est symétrique par rapport à l’axe des ordonnées. Par symétrie, il suffit donc de connaitre la fonction cosinus sur $[0; + \infty [$ pour la tracer pour tout réel.
$\sin(-x) = – \sin(x)$. On dit que la fonction sinus est impaire.
La courbe représentative de la fonction sinus est symétrique par rapport au centre du repère $O$, c’est donc une symétrie centrale. Par symétrie, il suffit donc de connaitre la fonction sinus sur $[0; + \infty [$ pour la tracer pour tout réel.
b) Propriété de périodicité des fonctions cosinus et sinus
A tout nombre réel $M$ sur le cercle correspond une infinité de points sur la droite des réels. En effet, lorsque la droite a été enroulée une fois, elle repasse au même endroit et associe donc un nouveau réel au point $M$.
La longueur d’enroulement pour revenir au même point $M$ correspond au périmètre du cercle trigonométrique de rayon $1$, c’est à dire $2 \pi$.
Ainsi, à un point sur le cercle correspond une infinité de points qui s’écrivent $x, x + 2\pi, x + 2\times 2\pi, …$.
c) Propriétés :
Pour tout nombre réel $x$, on a :
1) $\cos(x) = \cos(x + 2k \pi)$ où $k \in \mathbb{Z}$.
Comme $x$ et $x +2k\pi$ correspondent au même point sur le cercle, ils ont la même abscisse et donc le cosinus de ces nombres est égal.
2) $\sin(x) = \sin(x + 2k \pi)$ où $k \in \mathbb{Z}$.
Comme $x$ et $x +2k\pi$ correspondent au même point sur le cercle, ils ont la même ordonnée et donc le sinus de ces nombres est égal.
On dira alors que les fonctions cosinus et sinus sont périodiques de période $2\pi$.
En conséquence, pour étudier les fonctions cosinus et sinus, il suffit de les étudier sur un intervalle de longueur $2 \pi$ et l’on pourra en déduire les variations de la fonction sur son ensemble de définition par translation de période $2\pi$ des variations trouvées sur l’intervalle initial.
III) Dérivées, variations et courbes représentatives
Théorème (admis) :
Les fonctions $\cos$ et $\sin$ sont dérivables en $0$ et $\cos'(0) = 0$ (la courbe admet une tangente horizontale à l’origine) et $\sin'(0) = 1$ (la courbe admet une tangente de coefficient directeur 1 à l’origine).
Les fonctions $\cos$ et $\sin$ sont dérivables sur $\mathbb{R}$ et on a pour tout $x$ réel :
$\cos'(x) = – \sin(x)$
$\sin(x) = \cos(x)$
1) Etude de la fonction cosinus
On sait que $\cos'(x) = -\sin(x)$.
On se place sur l’intervalle $[0; \pi]$ et on calcule les valeurs aux bornes de la fonction sinus.
$\sin(0) = 0$ et $\sin(\pi) = 0$.
En outre, la fonction sinus est négative pour $x \in [0; \pi]$. La fonction cosinus es donc décroissante sur cet intervalle.
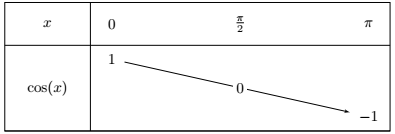
De plus, $\cos(0) = 1$, $\cos(\pi) = -1$ et $\cos \left ( \dfrac{\pi}{2} \right ) = 0$.
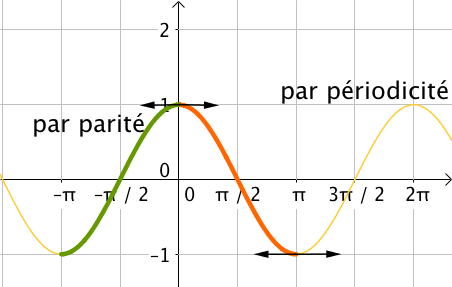
Ensuite, on en déduit les variations de la fonction sur $[-\pi; 0]$ par parité de la fonction.
Par symétrie par rapport à l’axe des ordonnées, on en déduit que la fonction cosinus est croissante sur cet intervalle.
Enfin, on conclut par $2\pi$ périodicité de la fonction pour étendre l’étude des variations de la fonction à l’ensemble des réels.
2) Etude de la fonction sinus
On sait que $\sin'(x) = \cos(x)$.
On se place sur l’intervalle $[0; \pi]$ et on calcule les valeurs aux bornes de la fonction cosinus.
$\cos(0) = 1$ et $\cos(\pi) = -1$.
On sait aussi que $\cos \left ( \dfrac{\pi}{2} \right ) = 0$.
La fonction cosinus est donc positive sur $\left [0; \dfrac{\pi}{2} \right ]$ et négative sur $\left [\dfrac{\pi}{2}; \pi \right ]$.
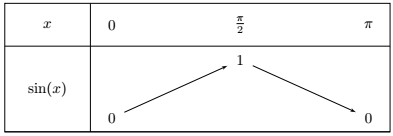
La fonction sinus est donc croissante sur $\left [0; \dfrac{\pi}{2} \right ]$ et décroissante sur $\left [\dfrac{\pi}{2}; \pi \right ]$.
De plus, $\sin(0) = 0$, $\sin(\pi) = 0$ et $\sin \left ( \dfrac{\pi}{2} \right ) = 1$.
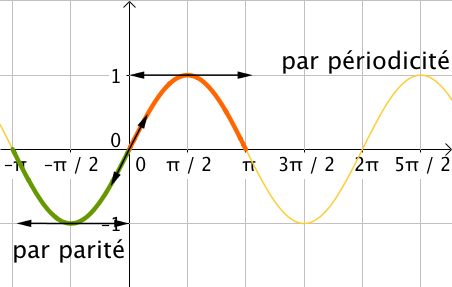
Ensuite, on en déduit les variations de la fonction sur $[-\pi; 0]$ car la fonction est impaire.
Par symétrie par rapport à l’origine du repère $O$, on en déduit que les variation de la fonction sinus sur cet intervalle.
Enfin, on conclut par $2\pi$ périodicité de la fonction pour étendre l’étude des variations de la fonction à l’ensemble des réels.