Probabilité d'une réunion
Probabilité d’une réunion
Propriété
$A\cap B$ est l’événement constitué des issues communes à $A$ et à $B$.
$A\cup B$ est l’événement constitué des issues appartenant à $A$ ou $B$.
$\boxed{ p(A\cup B)=p(A)+p(B)-p(A\cap B)}$
Si $A \cap B = \varnothing$ alors $p(A\cup B)=p(A)+p(B)$.
Exemple
Au mois d’août, un club comporte 300 vacanciers :
- 75 font de la planche à voile
- 129 font de la plongée
- 30 font les deux activités
Calculer la probabilité qu’un vacancier de ce club choisi au hasard pratique au moins une des deux activités.
- étape 1 : On reconnaît dans l’énoncé l’expression clé qui nous indique une réunion, ici ” au moins “.
- étape 2 : On distingue les événements présents dans l’énoncé :
$V$: “Le vacancier choisi au hasard qui pratique la voile “.
$P$: “Le vacancier choisi au hasard qui pratique la plongée “.
- étape 3 : On applique la formule du cours sur la probabilité d’une réunion :
$p(V\cup P)=p(V)+p(P)-p(V\cap P)$
$p(V\cup P)= \dfrac{75}{300}+\dfrac{129}{300}-\dfrac{30}{300}$
$p(V\cup P)=0,58$
Probabilité d'une réunion - Exercice
Exercice
Au mois d’août, un club comporte 300 vacanciers :
- 75 font de la planche à voile
- 129 font de la plongée
- 30 font les deux activités
Calculer la probabilité qu’un vacancier choisi au hasard pratique au moins une des deux activités.
- Étape 1 : On reconnaît dans l’énoncé l’expression clé qui nous indique une réunion, ici “au moins”.
- Étape 2 : On distingue les événements présents dans l’énoncé.
- Étape 3 : On applique la formule du cours sur la probabilité d’une réunion :
\(P(A \cup B) = P(A) + P(B) – P(A \cap B)\)
Formule des probabilités totales
Formule des probabilités totales
Définition
Une partition de $\Omega$ est un ensemble de parties de $\Omega$ deux à deux disjointes et dont la réunion est $\Omega$.
Propriété
Si $B_1 , B_2\ldots,B_n$ forment une partition de $\Omega$, alors, pour tout événement $A$, on a:
$p(A)= p(A\cap B_1) + p(A\cap B_2)+\ldots + p(A\cap B_n)$
Exemple
Un sac contient des jetons de 3 couleurs différentes : blancs (50%), verts (25%) et jaunes (25%).
Les jetons peuvent être ronds ou carrés.
La moitié des jetons blancs sont ronds, 70% des jetons verts sont carrés et 4 jetons jaunes sur 10 sont ronds.
On choisit un jeton au hasard. Quelle est la probabilité que le jeton soit rond ?
On note les événements :
$B$ : “Le jeton est blanc “.
$V$ : “Le jeton est vert “.
$J$ : “Le jeton est jaune “.
$R$ : “Le jeton est rond “.
$C$ : “Le jeton est carré “.
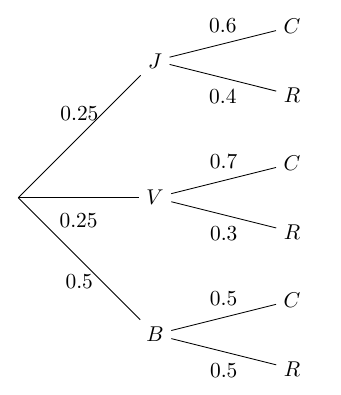
- étape 1 : On réalise un arbre de probabilité afin de mieux visualiser chaque situation.
- étape 2 : On remarque que les événements $B, V$ et $J$ forment une partition de l’univers (et il faut l’écrire !).
- étape 3 : On applique la formule des probabilités totales.
$p(R)= p(B\cap R) + p(J\cap R)+p(V\cap R)$
$p(R)= p(B)\times p_{B}(R) + p(J)\times p_{J}(R)+ p(V)\times p_{V}(R)$
$p(R)= 0,5\times 0,5 + 0,25 \times 0,3 + 0,25\times 0,4$
$p(R) = 0,425$
La probabilité que le jeton soit rond est égale à 0,425.
Formule des probabilités totales - Exercice
Exercice
Un sac contient des jetons de 3 couleurs différentes : blancs (50%), verts (25%) et jaunes (25%).
Les jetons peuvent être ronds ou carrés. On choisit un jeton au hasard. Quelle est la probabilité que le jeton soit rond ?
- Étape 1 : On réalise un arbre de probabilité afin de mieux visualiser chaque situation.
- Étape 2 : On remarque que les événements B, V et J forment une partition de l’univers (et il faut l’écrire !).
- Étape 3 : On applique la formule des probabilités totales.