Inégalité triangulaire
Inégalité triangulaire
Propriété
Dans un triangle, la longueur d’un côté est inférieure à la somme des deux autres.
Exemple :
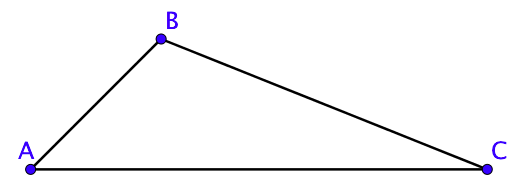
Dans le triangle $ABC$, on a
- $AB < AC + BC$
- $BC < BA + AC$
- $AC < AB + BC$.
En d’autres termes, cela signifie que pour relier deux points, le chemin le plus court est la ligne droite plutôt que le détour.
Cas particulier :
Si $AB = AC + CB$, alors le point $C$ appartient au segment $[AB]$.
En d’autres termes, le chemin pour aller de $A$ vers $B$ est aussi long que celui passant par $C$, cela signifie que le point $C$ est sur le chemin, et donc que les points sont alignés.
Constructions de triangles
L’inégalité triangulaire permet de vérifier qu’un triangle est constructible ou non.
En effet, si un côté est plus grand que la somme des deux autres alors le triangle n’est pas constructible car les deux arcs de cercle ne se croiseront pas.
Exemples :
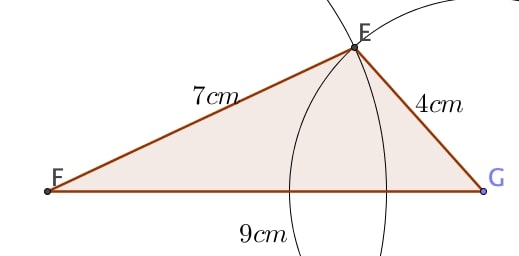
1) On souhaite tracer un triangle $EFG$ tel que $EF = 7$ cm, $FG = 9$ cm et $EG= 4$ cm.
Pour vérifier que le triangle est constructible, il suffit de s’assurer que l’inégalité triangulaire est vérifiée pour chaque côté.
On vérifie que :
- $7<4+9$
- $9<7+4$
- $4<7+9$
Ce triangle est donc constructible.
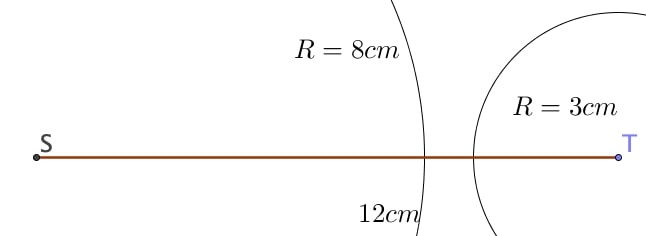
2) On souhaite tracer un triangle $RST$ tel que $RS = 8$ cm, $ST = 12$ cm et $RT = 3$ cm.
Le plus grand côté est $[ST]$ et il mesure $12$ cm.
On calcule ensuite séparément la somme des deux autres côtés $RS + RT = 8 + 3 = 11 < 12$.
Ainsi, $RS + RT < ST$,
Le triangle $RST$ n’est donc pas constructible.
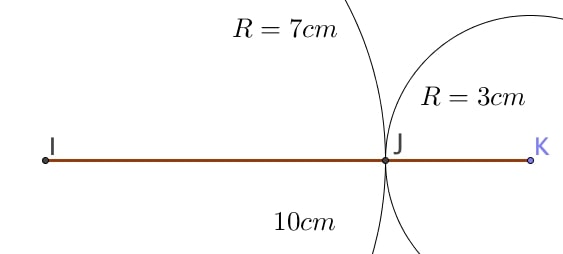
3) On souhaite tracer un triangle $IJK$ tel que $IJ = 7$ cm, $JK = 3$ cm et $IK = 10$ cm.
Le plus grand côté est $[IK]$ et il mesure $10$ cm.
On calcule ensuite séparément la somme des deux autres côtés
$IJ + JK = 7 + 3 = 10 $.
Ainsi, $IK = IJ + JK$.
Cela signifie que le point $J$ appartient au segment $[IK]$.