Inéquations produit, tableau de signes
Inéquations produit
On souhaite résoudre l’inéquation suivante $(2x + 1)(1 – 3x) \geq 0$.
Il est bon de s’interroger sur l’existence d’une solution.
Si le premier facteur est positif, ainsi que le second, alors par produit, le résultat est positif.
De même, si le premier facteur est négatif, ainsi que le second, alors par produit, le résultat est positif.
Néanmoins, si les deux facteurs n’ont pas le même signe, il n’existe pas de solution.
On étudie donc le signe de chaque facteur en fonction de $x$.
On cherche donc tout d’abord pour quels $x$ le facteur $2x + 1$ est positif ou nul, ou encore, on veut résoudre $2x + 1 \geq 0$.
Cela revient à écrire que $2x \geq -1$ ou encore $x \geq \dfrac{-1}{2}$. Ainsi, si $x \geq \dfrac{-1}{2}$, on a $2x + 1 \geq 0$.
De même, on veut résoudre $1 – 3x \geq 0$, c’est à dire $-3x \geq -1$ soit $x \leq \dfrac{1}{3}$ (il faudra prêter attention au fait que multiplier ou diviser par un nombre négatif change le sens de l’inégalité).
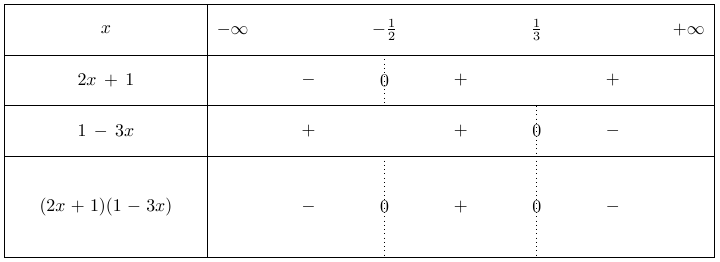
On reporte ensuite les informations trouvées précédemment dans un tableau de signe.
On indique dans la première ligne les valeurs de $x$ classées par ordre croissant, c’est à dire les valeurs calculées.
En dessous des valeurs $\dfrac{-1}{2}$ et $ \dfrac{1}{3}$, on trace un trait vertical.
La deuxième ligne contient le signe de $2x + 1$ sur les différents intervalles.
En reprenant le premier calcul, on a montré que $2x + 1$ était positif si $x \geq \dfrac{-1}{2}$ : on indique donc les cases à droite de $\dfrac{-1}{2}$ un signe $+$ pour indique que la positivité du nombre pour les valeurs de $x$ considérées.
Il reste ensuite à écrire un signe $-$ dans la case non remplie pour signifier que $2x + 1$ est négatif ici.
Enfin, sur le trait correspondant (c’est à dire celui associé à $x = \dfrac{-1}{2}$, on indique un $0$ pour signifier la nullité de l’expression.
La troisième ligne indique le signe de $1 – 3x$.
Pour la remplir, on utilise le calcul trouvant à quelles conditions $1 – 3x$ est positif : on avait alors trouvé que cela se réalisait pour $x \leq \dfrac{1}{3}$, c’est à dire des nombres plus petits que $\dfrac{1}{3}$.
On écrit donc des signes $+$ dans les cases à gauche de $dfrac{1}{3}$.
Enfin, pour remplir la dernière ligne, qui donne le signe du produit en utilisant la règle des signes pour les produits.
Pour répondre à notre question initiale, à savoir résoudre l’inéquation $(2x + 1)(1 – 3x) \geq 0$, on utilise le tableau de signe en gardant uniquement les intervalles pour lesquelles le signe est un $+$, c’est à dire
$S = \left [\dfrac{-1}{2}; \dfrac{1}{3} \right ]$.