Le cercle au collège
Le cercle au collège
Vocabulaire
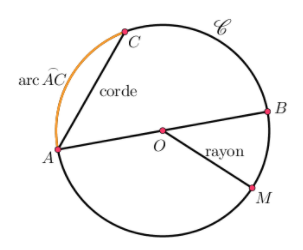
Un cercle $\mathscr{C}$ est défini par un centre $O$ et par un rayon $r$ qui est une longueur.
Ainsi, la distance entre un point $M$ sur le cercle et le centre du cercle est égale au rayon.
Un cercle est donc l’ensemble des points à égale distance du centre, cette distance étant appelée le rayon.
En d’autres termes, l’ensemble de ces points est équidistant du centre.
On note : $OM=r$
L’arc $\overset{\frown}{AC}$, est la portion du cercle entre les points $A$ et $C$ du cercle et la corde est le segment reliant deux points du cercle.
La corde passant par le centre est la plus grande : c’est un diamètre du cercle et a pour longueur le double du rayon.
Cercle circonscrit à un triangle
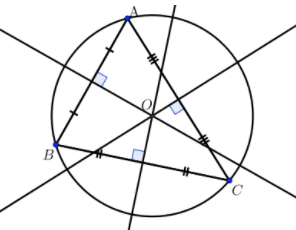
Le cercle circonscrit à un triangle est le cercle qui passe par les trois sommets du triangle.
Le centre du cercle est donc équidistant des sommets du triangle.
Afin de trouver ce centre, il faut tracer les médiatrices des triangles, qui sont les droites passant par le milieu des côtés perpendiculairement et le centre se trouve au point de concours des médiatrices.
Propriété dans le triangle rectangle
Si $ABC$ est un triangle rectangle en $C$, alors le centre du cercle circonscrit est le milieu de l’hypoténuse $[AB]$.
Ainsi, pour trouver le centre du cercle circonscrit d’un triangle rectangle, il suffit de trouver le milieu de l’hypoténuse.
Si $A \in \mathscr{C}, B \in \mathscr{C}, C \in \mathscr{C}$ et si un des côtés est un diamètre du cercle, alors le triangle $ABC$ est rectangle.