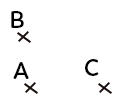Lentille convergente
Lentille convergente
I. Pourquoi convergente ?
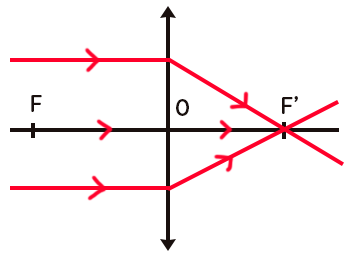
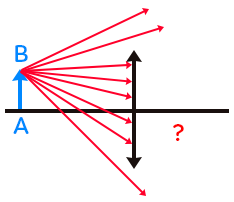
Un schéma typique en optique est composé d’un axe optique, d’un trait vertical avec deux chevrons qui représente la lentille convergente, et des rayons arrivant sur la lentille. Ces rayons parallèles à l’axe optique convergent alors vers le foyer image $F’.$ Le symétrique de $F’$ par rapport à $O$ est appelé foyer objet et est noté $F.$
II. Distance algébrique
Souvent une distance est positive, mais en optique ce n’est pas le cas. On ajoute une notion de direction à ces distances, et pour cela une convention est prise. Lorsque l’on va vers la droite et/ou vers le haut les distances sont positives, sinon elles sont négatives.
Exemple :
De manière classique nous avons $AB=BA>0.$ En optique la distance algébrique se note $\overline{AB}$ et on a :
$\overline{AB}>0$ mais $\overline{BA}<0$ ainsi que $\overline{AC}>0$ mais $\overline{CA}<0$.
En effet, pour $\overline{AB}$ la direction est de $A$ vers $B,$ c’est-à-dire dans le sens positif.
III. Distance focale
La distance focale est une caractéristique de la lentille, elle est noté $f’$ et elle vaut $f’=\overline{OF’}$.
Elle s’exprime en mètre (m).
Pour une lentille convergente, $f’>0$ car le foyer image $F’$ est à droite de $O$ donc la distance algébrique est positive.
IV. Trois rayons particuliers
Il est très important de connaître ces trois rayons particuliers :
Le rayon arrivant parallèle à l’axe optique : celui-ci sort après la lentille en passant forcément par le foyer image $F’.$
Le rayon passant par le centre optique $O$ : celui-ci n’est pas dévié, il continue sa trajectoire après le passage par la lentille.
Le rayon passant par le foyer objet $F$: celui-ci sort parallèle à l’axe optique après la lentille.
Image réelle d'un objet réel
Image réelle d’un objet réel
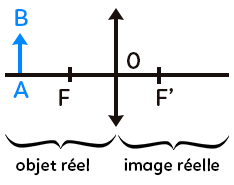
I. Objet réel
La notion d’objet réel fait opposition à celle d’objet virtuel. Un objet est repéré par deux extrémités : 2 points $A$ et $B$ orientés de $A$ vers $B.$ Un objet est réel lorsqu’il se trouve à gauche de la lentille convergente, et une image est réelle lorsqu’elle se trouve à droite de la lentille convergente. Si l’image se trouvait à gauche, alors elle serait qualifiée de virtuelle, et de même un objet est virtuel lorsqu’il est à droite de la lentille (derrière la lentille).
II. Modèle du rayon lumineux
Dans un milieu transparent et homogène, la lumière se déplace en ligne droite. Un milieu transparent est un milieu dans lequel la lumière peut passer (en opposition avec opaque). Un milieu est homogène, lorsque, en tous points du milieu, les caractéristiques sont les mêmes (en opposition avec hétérogène).
Par exemple, l’air est un milieu homogène mais le brouillard est un milieu hétérogène (il y des gouttes dans certains endroits et de l’air dans d’autres). Comme la lumière va en ligne droite, on peut tracer des droites pour représenter les rayons dans les schémas optiques : c’est le modèle du rayon lumineux.
III. L’objet diffuse de la lumière
L’objet $AB$ est forcément éclairé par une source de lumière, ainsi à son tour le point $B$ va rediffuser de la lumière. Il y a donc une multitudes de rayons partant du point $B$ dans toutes les directions. Un certain nombre de ces rayons lumineux passant par la lentille, on peut alors, grâce à des rayons particuliers, déterminer la position et la taille de l’image réelle de l’objet $AB.$
IV. L’image de l’objet AB
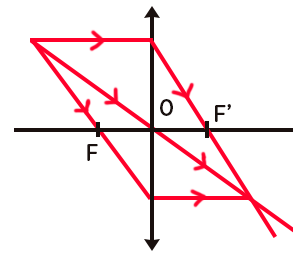
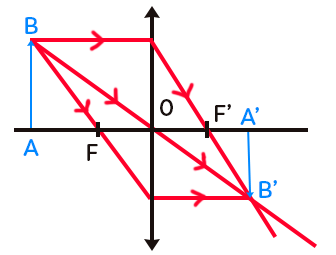
Pour déterminer l’image réelle $A’B’$ il faut utiliser les trois rayons particuliers qui partent de $B$ :
– Celui qui est parallèle à l’axe optique, il sera alors dévié pour passer par le foyer image $F’.$
– Celui qui passe par le centre optique $O$, il n’est pas dévié.
– Celui qui passe par le foyer objet $F’,$ il est ressort parallèle à l’axe optique après la lentille.
L’intersection de ces trois rayons est la position du point $B’,$ et en réalité seuls 2 sur 3 de ces rayons sont nécessaires. On dit alors que la lentille conjugue les points $B$ et $B’.$
Pour trouver $A’,$ il suffit de tracer une perpendiculaire à l’axe optique qui remonte de $B’, A’$ se trouve à l’intersection de cette perpendiculaire et de l’axe optique.
Pour ce qui est des distances algébriques, on voit que $\overline{AB}$ mais que $\overline{A’B’}$ est négative : l’image est donc renversée.
V. Le grandissement
Une notion mathématique est associée aux objet et image à travers une lentille : c’est le grandissement noté $\gamma$, il vaut : $\gamma=\dfrac{\overline{A’B’}}{\overline{AB}}$ et est sans unité car c’est un rapport entre 2 distances.
Exemple :
D’après le schéma du IV. on a : $\gamma=\dfrac{-6.5 \times 10^{-2}}{9 \times 10^{-2}}=-0.7$.
Il faut faire attention aux chiffres significatifs pour écrire un résultat correct. Ici, comme le numérateur a deux chiffres significatifs et le dénominateur un seul, on écrit un résultat avec un seul chiffre significatif.
Remarque :
Si $|\gamma |<1$ c’est-à-dire $-1< \gamma < 1$ alors l’image sera plus petite que l’objet.
Si $\gamma< 0 $ alors l’image est renversée.
Le modèle de l'œil
Le modèle de l’œil
I. Notion de modèle
Définition :
Un modèle est l’utilisation de blocs élémentaires connus pour simplifier un système complexe Comme un modèle simplifie un système complexe, il peut y avoir des limites.
Exemple :
On peut modéliser une voiture par seulement 4 roues, un moteur et un bas de caisse. Si on veut alors modéliser le fonctionnement des essuies-glace d’une voiture, on ne pourra pas le faire car c’est dans la limite du modèle.
II. Le modèle de l’œil
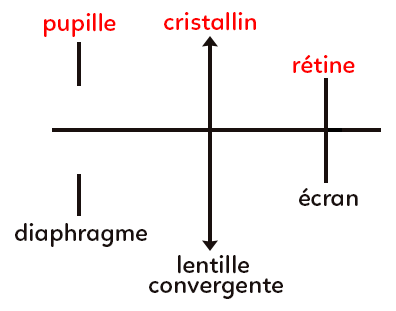
Lorsque la lumière arrive sur un œil, elle commence d’abord par traverser la cornée, puis l’iris au centre duquel il y a la pupille de l’œil. Derrière la pupille se trouve le cristallin qui fait converger les rayons lumineux, et grâce aux muscles ciliaires, il peut se déformer. Après le cristallin, la lumière va aller sur la rétine, c’est là que se trouvent les cellules photoréceptrices.
Le modèle de l’œil se résume à trois blocs :
– La lentille convergente modélise le cristallin.
– Le diaphragme modélise la pupille.
– L’écran modélise la rétine.
III. Utilisation du modèle
Ce modèle de l’œil permet de comprendre quel est le problème de la myopie.
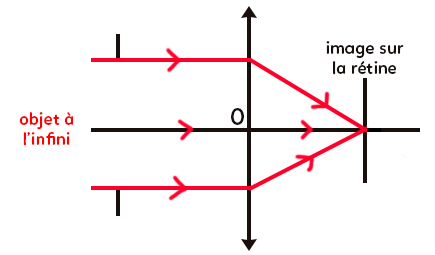
En effet, pour un œil normal, on a :
Lorsqu’un objet provient de l’infini (à partir d’une dizaine de mètres), les rayons arrivent parallèles entre eux sur la lentille convergente. Tous ces rayons vont converger vers le point focal image qui se trouve sur l’écran (la rétine).
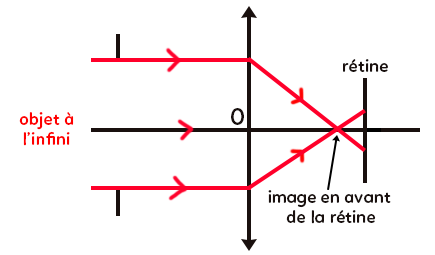
Pour un œil myope le schéma est le suivant :
Les rayons convergent trop vite, c’est-à-dire que la distance focale est trop petite, l’image se forme en amont de la rétine et donc la vision est floue.
Hors programme :
Une solution pour régler le problème de la myopie est de rajouter une lentille (un paire de lunettes) qui va faire diverger les rayons pour compenser la trop grande convergence de l’œil.
Remarque :
Pour le problème de l’hypermétropie, cette fois l’image se forme après la rétine, la distance focale est trop grande.