Limite d'une fonction en l'infini
Limite d’une fonction au voisinage de l’infini
Définitions
$\bullet$ Une fonction $f$ tend vers un réel $l$ quand $x$ tend vers $+\infty$ si, pour tout intervalle ouvert centré en $l$, il existe un réel $x_0$ tel que si $x\geqslant {x_0}$, alors $f(x)$ appartient à cet intervalle.
On notera $\displaystyle \lim_{x\to +\infty} f(x) = \ell$.
$\bullet$ Dans ce cas la droite d’équation $y=\ell$ est une asymptote horizontale à la courbe représentative de $f$ au voisinage de $+\infty$.
Ces définitions sont de même nature au voisinage de $-\infty$.
Limite au voisinage de $+\infty$
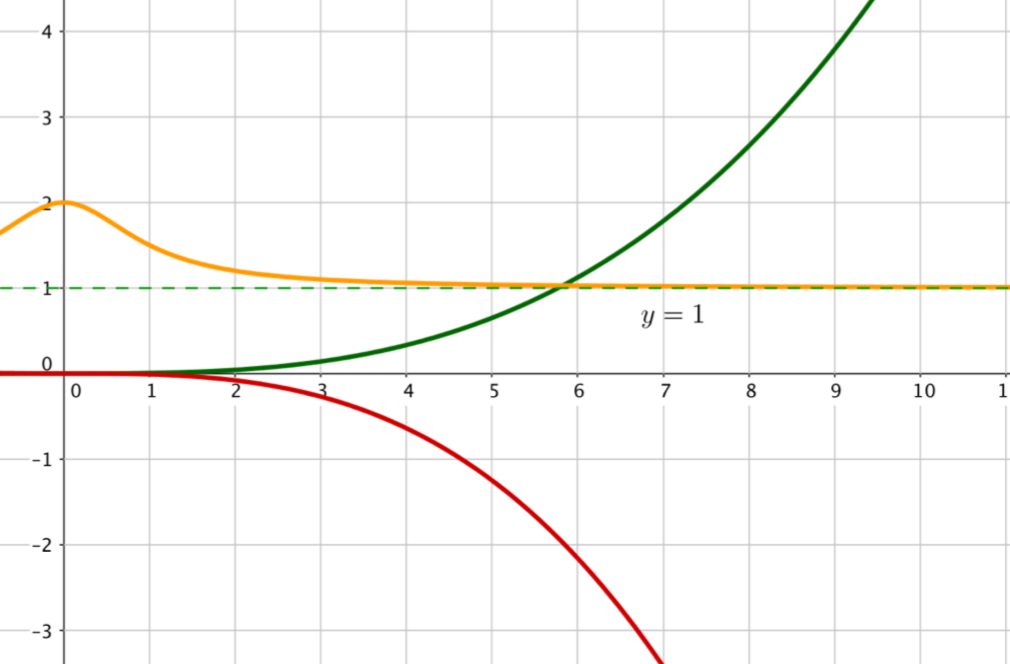
La fonction dont la courbe est en vert tend vers $+\infty$ lorsque $x$ tend vers $+\infty$.
En effet, on remarque que plus $x$ est grand, plus la valeur de $f(x)$ augmente sans que les valeurs de $f$ soient plafonnées.
La fonction dont la courbe est en rouge tend vers $-\infty$ lorsque $x$ tend vers $+\infty$.
En effet, on remarque que plus $x$ est grand, plus la valeur de $f(x)$ diminue.
La fonction dont la courbe est en orange tend vers $1$ lorsque $x$ tend vers $+\infty$.
En effet, on remarque que plus $x$ est grand, plus la valeur de $f(x)$ se rapproche de $1$.
Ici la droite d’équation $y=1$ est une asymptote horizontale à la courbe au voisinage de $+\infty$.
Limite au voisinage de $-\infty$
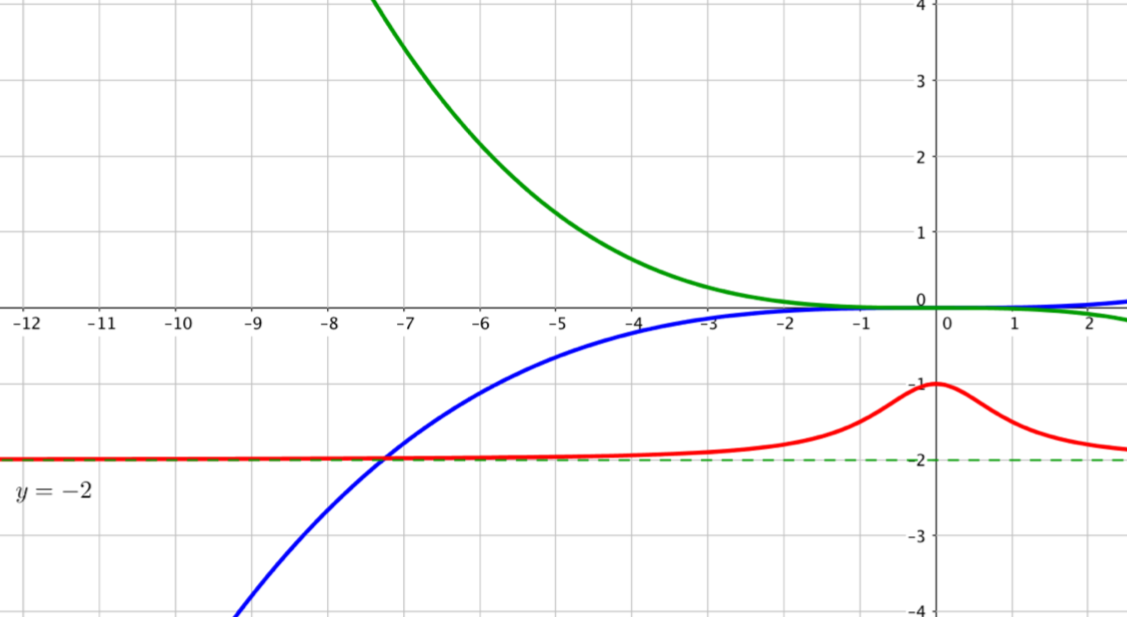
La fonction dont la courbe est en vert tend vers $+\infty$ lorsque $x$ tend vers $-\infty$.
En effet, on remarque que plus $x$ est petit, plus la valeur de $f(x)$ augmente.
La fonction dont la courbe est en bleu tend vers $-\infty$ lorsque $x$ tend vers $-\infty$.
En effet, on remarque que plus $x$ est petit, plus la valeur de $f(x)$ diminue.
La fonction dont la courbe est en rouge tend vers $-2$ lorsque $x$ tend vers $-\infty$.
En effet, on remarque que plus $x$ est petit, plus la valeur de $f(x)$ se rapproche de $-2$.
La droite d’équation $y=-2$ est une asymptote horizontale à la courbe au voisinage de $-\infty$.
Exemple de fonctions n’ayant pas de limite
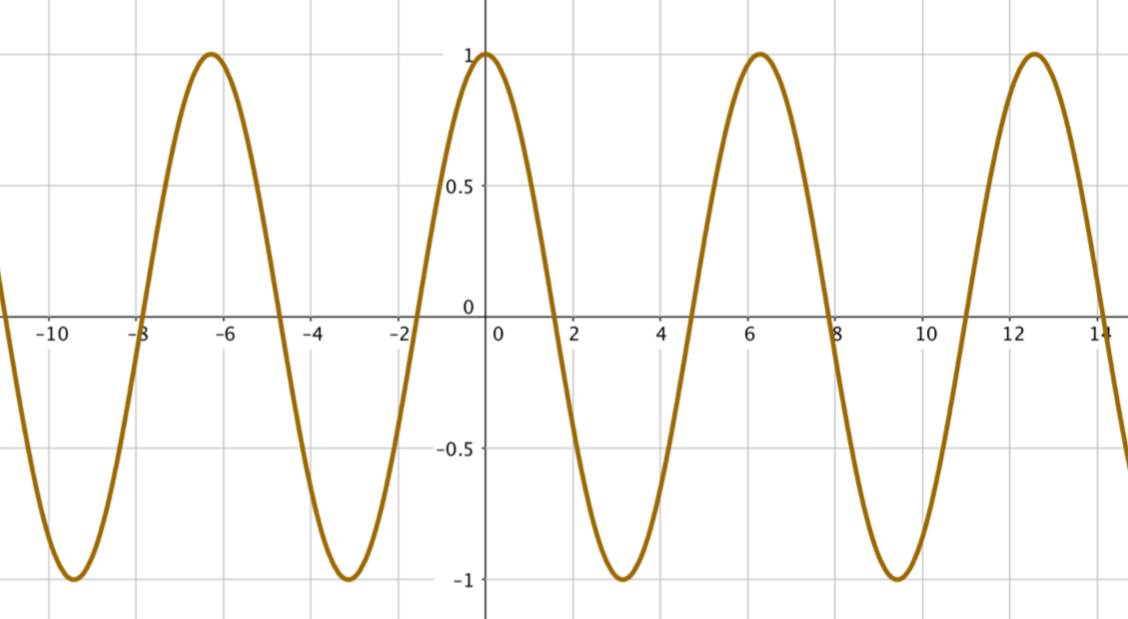
Certaines fonctions n’ont pas de limite en $+\infty$ ou en $-\infty$, par exemple parce qu’elles oscillent.
La fonction cosinus en marron est un exemple de ce genre de fonctions :
Le plus des Bons Profs
Un moyen de conjecturer la limite d’une fonction en $+\infty$ (respectivement en $-\infty$) est de calculer $f$ au point $x=1 000$ (respectivement $x=-1000$) ou, si cela n’est pas suffisant, au point $x=1 000 000$ (respectivement $x=-1 000 000$).
Limite d'une fonction en un réel a
Limite infinie d’une fonction en un réel a
Définitions
$\bullet$ Soit $a$ un réel. Une fonction $f$ tend vers $+\infty$ quand $x$ tend vers $a$ si, pour tout réel $A$, il existe un intervalle centré en $a$ tel que pour tous les $x$ appartenant à cet intervalle, on a : $f(x)>A$.
On note $\displaystyle \lim_{x\to a} f(x)=+\infty$.
$\bullet$ Si $\displaystyle \lim_{x\to a} f(x) = \pm \infty$ alors la droite d’équation $x=a$ est une asymptote verticale à la courbe représentative de $f$.
Ces définitions sont de même nature si $f$ tend vers $-\infty$ ou si on étudie les limites à gauche ou à droite de la fonction.
Illustrations graphiques
On va ici prendre en exemple le point $x=5$ mais les remarques et illustrations graphiques seront valables pour n’importe quel point $x=a$ avec $a\in \mathbb{R}$.
1)
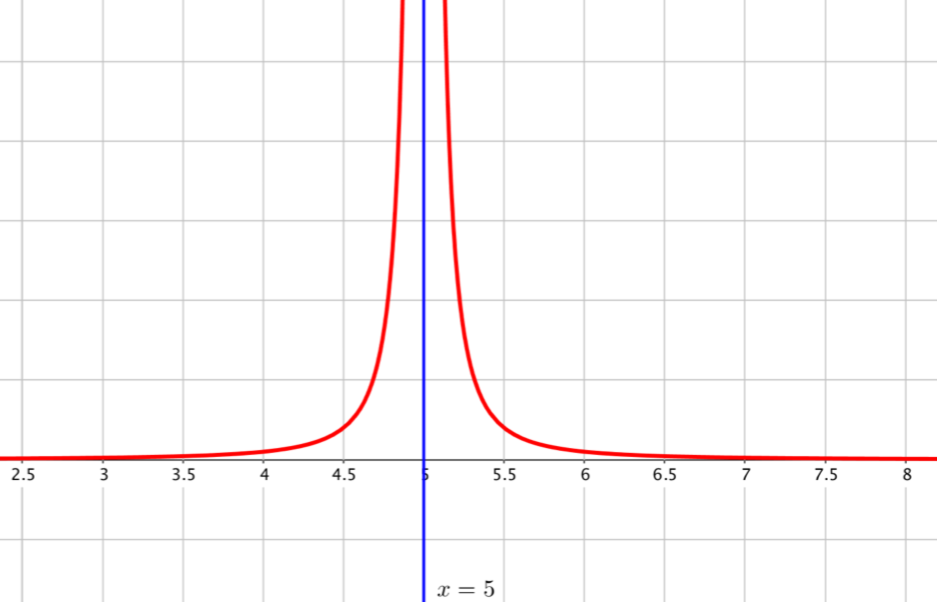
Sur la figure $1$, le nombre $x=5$ est une “valeur interdite” de la fonction représentée en rouge.
On constate que lorsque $x$ se rapproche de $5$ (par la droite ou par la gauche), $f(x)$ est de plus en plus grand.
On dit alors que $f$ tend vers $+\infty$ quand $x$ tend vers $5$ et on note $\displaystyle \lim_{x\to 5} f(x)=+\infty$.
Ici, et dans les deux cas suivants, la droite d’équation $x=5$ est une asymptote verticale à la courbe.
2)
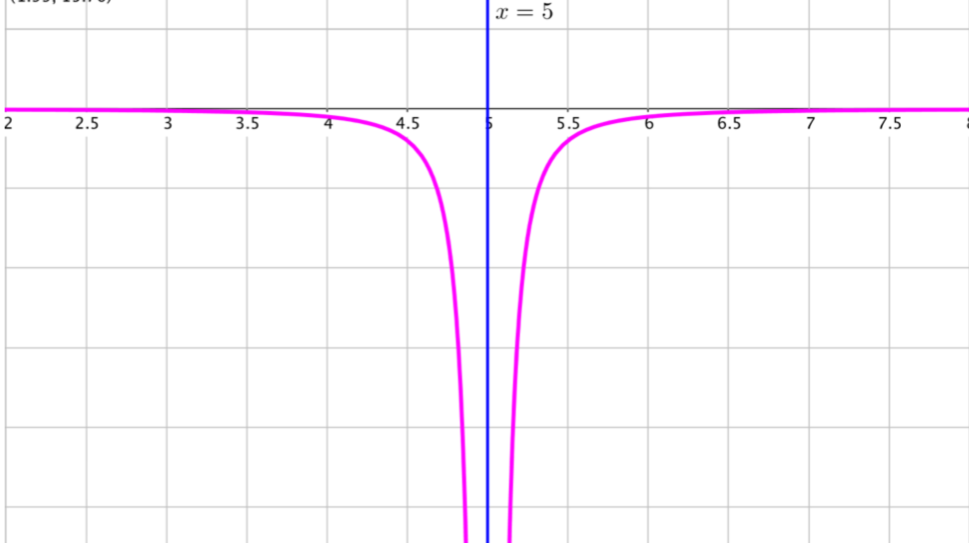
Sur la figure $2$, le nombre $x=5$ est une nouvelle fois une “valeur interdite” de la fonction représentée en violet.
On constate que lorsque $x$ se rapproche de $5$ (par la droite ou par la gauche), $f(x)$ est de plus en plus petit.
On dit alors que $f$ tend vers $-\infty$ quand $x$ tend vers $5$ et on note $\displaystyle \lim_{x\to 5} f(x)=-\infty$.
3)
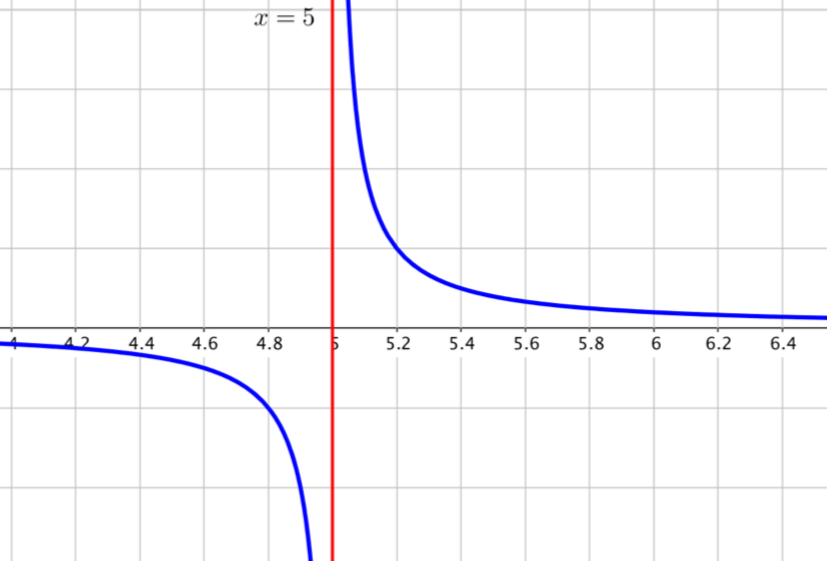
Le cas de la figure $3$ est différent. Certes le point $x=5$ est toujours une valeur interdite, mais la limite de la fonction représentée par la courbe bleu foncé n’est pas la même lorsqu’on s’approche soit par la gauche, soit par la droite de $x=5$.
On constate ici que $\displaystyle \lim_{\underset{x<5}{x\to 5}} f(x)=-\infty$ et $\displaystyle \lim_{\underset{x>5}{x\to 5}} f(x)=+\infty$.
Attention : Puisque les limites à gauche et à droite sont différentes, la $\displaystyle\lim_{x\to 5} f(x)$ n’existe pas.