Propriétés analytiques
Propriétés analytiques
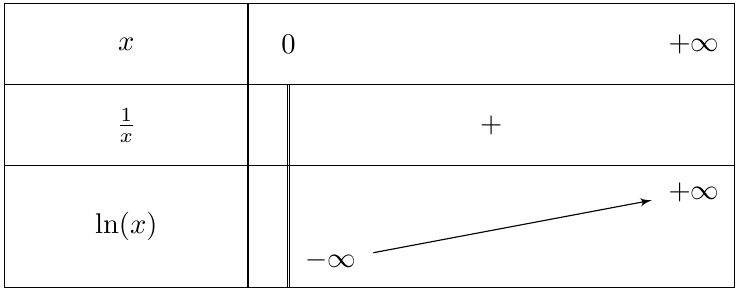
La fonction $\ln $ est définie et dérivable sur $]0;+\infty[$.
Pour tout réel $\displaystyle x>0, (\ln x)’= \dfrac{1}{x}$.
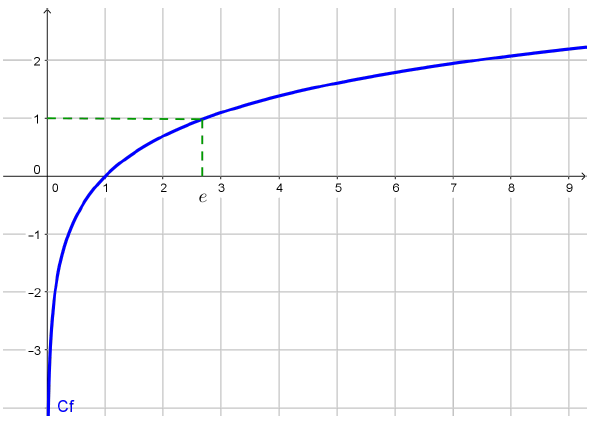
La fonction $\ln $ est continue et strictement croissante sur $]0;+\infty[$.
D’autre part,
$\ln (1)=0$
$\ln (e)=1$
$\displaystyle\lim\limits_{x \rightarrow +\infty} \ln x= +\infty$
$\displaystyle \lim_{\substack{x \to 0\\ x > 0}} \ln x=-\infty$
Variations et représentation graphique
Fonctions composées - ln (u(x))
Fonctions composées $\ln(u(x))$
Théorème
Soit la fonction $f$ définie sur l’intervalle $I$ par:
$\displaystyle f(x) = \ln(u(x))$ où $u$ est une fonction dérivable et strictement positive sur $I$,
alors $f$ est dérivable sur $I$ et $f'(x) = \displaystyle\dfrac{u'(x)}{u(x)}.$
Exemple
Déterminer l’ensemble de définition et la dérivée de la fonction $f$ définie par :
$\displaystyle f(x) = \ln(x^2+x+1)$
Le discriminant $\Delta = 1-4= -3$ donc
$x^2+x+1 > 0$.
La fonction est donc définie et dérivable sur $\mathbb{R}$.
Pour tout $x \in \mathbb{R}$, on a :
$u(x)=x^2+x+1$ et $u'(x)=2x+1.$
Alors : $f'(x) = \displaystyle\frac{2x+1}{x^2+x+1}$.
Pour étudier les variations de cette fonction, on pourra juste étudier le signe de $2x+1$
Fonctions composées - ln - Exercice 1
Exercice
Soit \(f(x) = ln(x^2 – 5x + 4) – ln(x – 5)\).
Cherchons l’ensemble de définition \(D_f\) de la fonction.
Étape 1 : On cherche les valeurs de \(x\) de sorte que les 2 expressions dans les logarithmes soient strictement positives.
Étape 2 : On regarde si on trouve une solution évidente : 1, -1, 2, -2, etc.
Étape 3 : On fait le tableau de signe du trinôme.
Fonctions composées - ln - Exercice 2
Étudions les variations de \(f(x) = ln(x^2 + x + 1)\)
Étape 1 : On cherche les valeurs de \(x\) de sorte que l’expression dans le logarithme soit strictement positive.
Étape 2 : On calcule le discriminant du polynôme.
Étape 3 : On distingue les deux fonctions composées. On pourra ainsi calculer \(u'(x)\).
Étape 4 : On dérive \(f'(x)\) à partir de la formule de dérivé d’une fonction composée avec un logarithme népérien.
Étape 5 : On cherche le signe de la dérivée à partir de son numérateur pour définir le sens de variation de la fonction.