Image d'un nombre par une fonction
Image d’un nombre par une fonction
Notion intuitive d’image
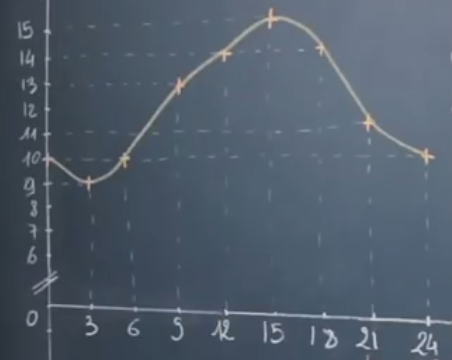
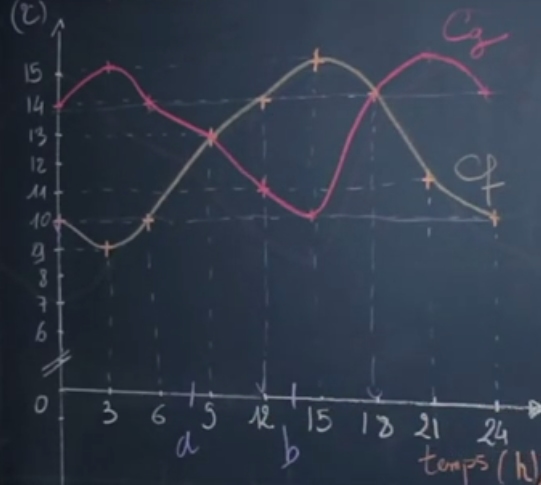
Considérons la courbe de température suivante :
L‘ensemble de définition de la fonction est $[0, 24]$, c’est à dire que l’étude se fait sur une journée complète à partir de minuit.
L’ordonnée est la température, il s’agit donc de la représentation graphique de la température en fonction du temps.
Ainsi, le temps est sur l’axe des abscisses.
Question : quelle température faisait-il à 3h du matin ?
On lit graphiquement que la température à 3h du matin est 9°C.
Ainsi, on dira que l’image de 3 par la fonction $f$ vaut 9 : il n’y a plus d’unité. On notera aussi $f(3) = 9$.
Définition
Soit $f$ une fonction et $a$ et $b$ deux réels vérifiants $f(a)=b$.
On dit que $b$ est l’image de $a$ par $f$.
Ou encore : l’image de $a$ par $f$ vaut $b$.
Autre exemple :
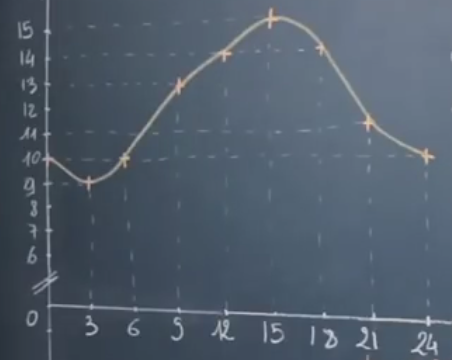
Pour trouver l’image de 15, on se place sur l’axe des abscisses à $t = 15$ puis on trace la droite perpendiculaire à cet axe et on regarde l’ordonnée du point d’intersection entre cette droite et la courbe de $f$ :
On lit $f(15) = 15$.
Antécédent d'un nombre par une fonction
Antécédent d’un nombre par une fonction
Définition
Soit $f$ une fonction et deux réels $a$ et $b$ vérifiant $f(a)=b$
On dit que $b$ est l’image de $a$ par $f$. (c’est une valeur unique)
On dit que $a$ est un antécédent par $f$ de $b$. (il peut y en avoir plusieurs)
Exemples
Cherchons le ou les antécédents, s’ils existent de $14$
Cela revient à chercher l’heure à laquelle la température était de 14°C.
Pour ce faire, on se place sur l’axe des ordonnées (l’axe des températures ici) et on trace la droite perpendiculaire à cet axe puis on regarde les points d’intersection entre la droite et la courbe de température et finalement, on lit leur abscisse.
Ici, il y a deux points d’intersections pour lesquels la température est de 14°C et donc deux heures différentes : 12h et 18h.
Il se peut que dans certains cas il n’y ait aucune solution.
Mathématiquement, le fait qu’il ait fait 14°C à 12h et 18h se traduit par :
Les antécédents de 14 par la fonction $f$ sont 12 et 18.
Ou encore : les solutions de l’équation $f(t) = 14$ sont $S = \{12; 18\}$.
Considérons l’équation $f(t) = 10$ : on cherche donc les antécédents de 10 par $f$.
Les solutions sont donc $S = \{0; 6; 24\}$.
Considérons l’équation $f(t) = 16$ : on cherche donc les antécédents de 16 par $f$.
La température de 16°C n’étant jamais atteinte, cette équation n’admet pas de solution :
$S = \varnothing$.
Résolutions graphiques d'équations
Résolutions graphiques d’équations
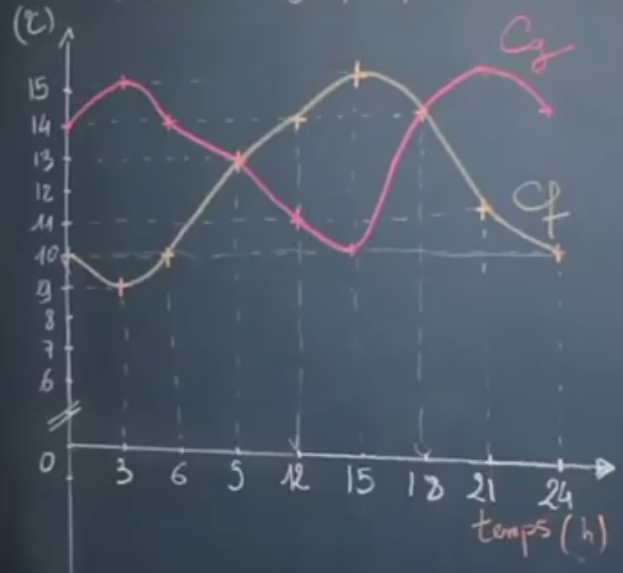
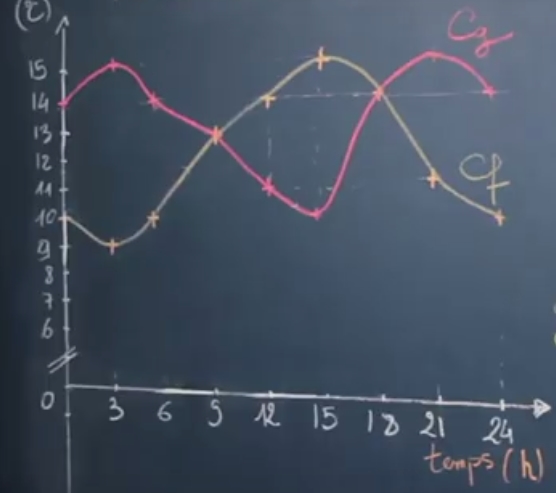
Considérons deux fonctions $f$ et $g$ représentant la température au cours du temps dans deux villes différentes.
Equations du type $f(t)=k$ avec $k\in \mathbb{R}$
Résoudre l’équation $f(t) = 14$ revient à chercher les antécédents de 14 par la fonction $f$.
Pour se faire, on se place sur l’axe des ordonnées(l’axe des températures ici) et on trace la droite perpendiculaire à cet axe puis on regarde les points d’intersection entre la droite et la courbe de température et finalement, on lit leur abscisse.
Ici, il y a deux points d’intersections pour lesquels la température est de 14°C et donc deux heures différentes : 12h et 18h. Ainsi $S = \{12; 18\}$.
Résoudre l’équation $f(t) = 8$ revient à chercher les antécédents de 8 par la fonction $f$.
Or il ne fait jamais 8°C, c’est à dire que la droite perpendiculaire à l’axe des ordonnées passant par $y = 14$ ne coupe jamais la courbe de $f$.
Ainsi $S = \varnothing$ et dans ce cas, il n’y a pas besoin d’accolades car $\varnothing$ signifie ensemble vide.
Résoudre l’équation $g(t) = 14$ revient à chercher les antécédents de 14 par la fonction $g$. Graphiquement, on trouve $S = \{0; 6; 18; 24\}$.
Equations du type $f(t)=g(t)$
Il est aussi attendu de savoir résoudre graphiquement l’équation $f(t) = g(t)$ en d’autres termes, il s’agit de trouver pour quelles valeurs de $t$ les deux températures sont égales :
les températures sont identiques aux points d’intersections des deux courbes. Ainsi $S = \{9; 18 \}$.
Résolutions graphiques d'inéquations
Résolutions graphiques d’inéquations
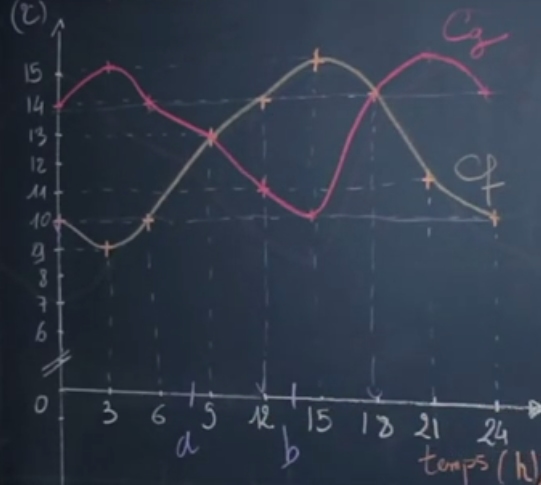
Considérons deux fonctions f et g représentant la température au cours du temps dans deux villes différentes entre 0 et 24h.
Inéquations du type $f(t)\geq k$
a) On cherche tout d’abord à résoudre l’inéquation $f(t) \geq 14$, c’est à dire on cherche les valeurs du temps où la température est supérieure ou égale à 14°C.
On cherche donc les abscisses pour lesquelles la courbe représentative de la fonction $f$ est au-dessus de la droite d’équation $ y = 14$ ou la coupe.
Ainsi, $S = [12; 18]$ : la température est supérieure à 14°C entre midi et 18h.
b) Les solutions de l’inéquation $f(t) \leq 8$ sont $ S = \varnothing$ car la température n’est jamais inférieure à 8°C.
c) On cherche à résoudre l’inéquation $g(t) < 14$, c’est à dire les abscisses pour lesquelles la courbe représentative de la fonction $g$ est strictement en-dessous de la droite d’équation $ y = 14$ : on ne retient donc pas les instants où la température vaut 14°C. Ainsi, $S = ]6; 18[$.
Inéquations du type $f(t)\geq g(t)$
Enfin l’inéquation $f(t) \geq g(t)$ revient à chercher les abscisses pour lesquelles la courbe représentative de la fonction $f$ est au dessus de celle de $g$, soit $ S = [9; 18]$.
Il faudra prêter une attention particulière à l‘orientation des crochets (intervalles ouverts ou fermés).
Maximum, minimum d'une fonction
Maximum, minimum d’une fonction
Une situation concrète
Soient $f$ et $g$ deux fonctions représentant l’évolution de la température au cours du temps.
Pour trouver le maximum de $f$, il faut regarder à quel instant la température est maximale. Il est atteint à $t = 15$.
Pour trouver le minimum de $f$, il faut regarder à quel instant la température est minimale. Il est atteint à $t = 3$.
Définition
Soit $f$ une fonction définie sur $D$, son ensemble de définition.
1) $M$ est un maximum de $f$ si pour tout $t \in D$, $f(t) \leq M$.
2) $m$ est un minimum de $f$ si pour tout $t \in D$, $f(t) \geq m$.
En d’autres termes, cette première inégalité signifie que la température est toujours plus petite que $M$ qui est le maximum.
On utilise la variable $t$ car on regarde l’évolution en fonction du temps, mais dans la plupart des cas, la variable utilisée sera $x$ sans que cela change la définition du maximum.
Le maximum de $f$ sur $[0; 24]$ est 15 et il est atteint en $t = 15$.
La température maximale est donc de 15°C et est atteinte à 15h.
Le minimum de $f$ sur $[0; 24]$ est 9 et il est atteint en $t = 3$.
Fonctions croissantes, décroissantes
Fonctions croissantes, décroissantes
Fonctions croissantes, décroissantes
Définitions.
Soit $f$ une fonction définie sur un intervalle $I$.
a) Pour tous réels $a$ et $b$ appartenant à $I$ tels que $a \leq b$,
si $f(a) \leq f(b)$ alors la fonction est croissante.
b) Pour tous réels $a$ et $b$ appartenant à $I$ tels que $a \leq b$,
si $f(a) \geq f(b)$ alors la fonction est décroissante.
Exemples
Soient deux fonctions $f$ et $g$ représentant l’évolution de la température en fonction du temps.
Considérons la fonction $f$ sur $[3; 15]$.
$f$ est croissante sur cet intervalle, la température augmente entre 3h et 15h.
Considérons de même la fonction $g$ sur $[3; 15]$.
$g$ est décroissante sur cet intervalle, la température diminue entre 3h et 15h.
Tableaux de variations
Tableaux de variations
Les tableaux de variation utilisent les notions de maximum, minimum et de fonctions croissante, décroissante et retranscrivent les variations de la fonction considérée.
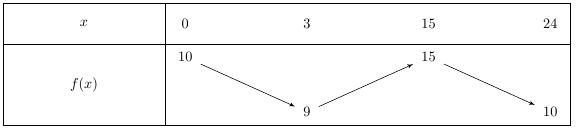
Un tableau de variation se présente toujours de la même façon. Voici un exemple pour les fonctions suivantes :
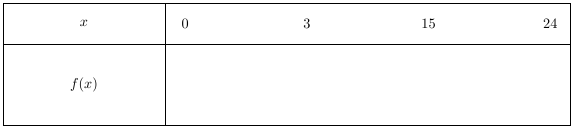
Etapes pour construire un tableau de variations
1) Sur la ligne du haut se trouvent les valeurs de la variable variant entre les bornes de l’ensemble de définition de la fonction.
Ici de $0$ à $24$.
Il faut ensuite regarder les valeurs de la variable pour lesquelles il y a un changement de variations, c’est à dire les points où la fonction admet un maximum ou minimum local.
Puis il faut placer ces valeurs dans la première ligne du tableau.
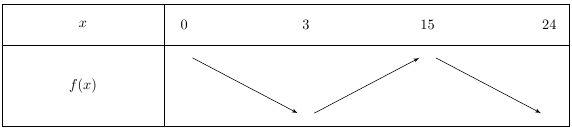
Ici, la fonction $f$ change de sens de variations (elle est d’abord décroissante puis croissante) en $t = 3$ et change à nouveau en $t = 15$.
2) Puis, pour symboliser que la fonction est décroissante sur l’intervalle $[0; 3]$ on trace une flèche vers le bas, puis une flèche vers le haut pour représenter la croissance de la fonction entre $[3; 15]$ puis à nouveau une flèche vers le bas entre $[15; 23]$.
3) Enfin, aux extrémités des flèches, il faut écrire l’image par la fonction $f$ des nombres inscrits sur la première ligne.
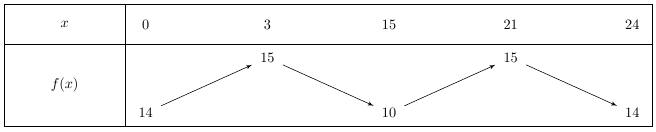
De même pour $g$, les points intermédiaires où la fonction change de sens de variation sont $3; 15; 21$.