Nombre dérivé
Nombre dérivé
Définition :
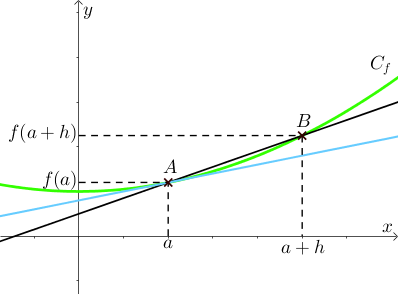
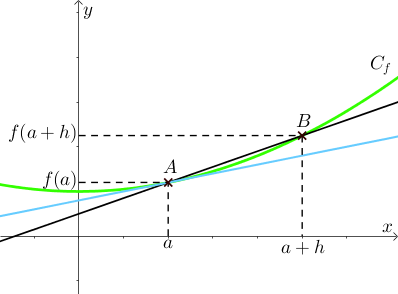
Soient $f$ une fonction définie sur $I$ et $a$ et $b$ deux points appartenant à la courbe représentative de la fonction $f$ ayant pour coordonnées respectives $(a; f(a))$ et $(a+h; f(a+h))$ où $h$ est un réel,
le coefficient directeur de la droite $(AB)$ est $\dfrac{y_B – y_A}{x_B – x_A} = \dfrac{f(a+h) – f(a)}{a + h – a} = \dfrac{f(a+h) – f(a)}{h}$ : c’est aussi le taux d’accroissement.
Le réel $h$ est choisi de plus en plus petit de telle manière que le point $B$ se rapproche du point $A$ et que la droite $(AB)$ se rapproche de la droite bleue.
On notera alors $\lim \limits_{h \to 0} \dfrac{f(a+h) – f(a)}{h}$.
Si le résultat de ce calcul est un réel $l$, alors la fonction $f$ est dérivable en $a$ et $l$ est noté $f'(a)$ :
$f'(a)$ est le nombre dérivé de la fonction $f$ au point $a$.
Exemple :
On considère $f(x) = x^2$.
Soit $a$ un réel,
on commence par calculer le taux d’accroissement
$\dfrac{f(a+h) – f(a)}{h} = \dfrac{(a+h)^2 – a^2}{h} = \dfrac{a^2 + 2ah + h^2 – a^2}{h} = 2a + h \text{ après simplification par } h$.
Puis on calcule la limite de ce taux d’accroissement, $\lim \limits_{h \to 0} \dfrac{f(a+h) – f(a)}{h} = 2a$.
Or $2a$ est un nombre fini, donc la fonction $f$ est dérivable en $a$ et $f'(a) = 2a$.
Tangente à une courbe en un point
Tangente à une courbe en un point
Soit $f$ une fonction définie sur $I$ et $a \in I$,
La limite du taux d’accroissement en un point $a$ lorsqu’elle existe donne le nombre dérivée de la fonction $f$ en $a$ :
$\lim \limits_{h \to 0} \dfrac{f(a+h) – f(a)}{h} = f'(a)$.
L’équation de la droite tangente à la courbe au point $a$ est
$T_a : y = f'(a)(x – a) + f(a)$.
Exemple :
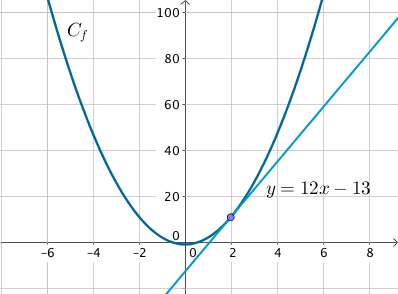
Soit $f(x) = 3x^2 -1$, on cherche l’équation de la tangente à la courbe au point d’abscisse $x =2$.
On calcule $f(2) = 11$.
On calcule ensuite la dérivée $f'(x) = 3 \times 2x = 6x$.
Ainsi, $f'(2) = 12$.
Graphiquement le nombre dérivé de la fonction en un point $a$ est le coefficient directeur de la tangente au point d’abscisse $a$.
Enfin,
$T_2 : y = f'(2)(x – 2) + f(2)$
$y = 12(x – 2) + 11$
$y = 12x – 13$
Dérivées usuelles
Dérivées usuelles
Définition :
Soient $f$ une fonction définie sur $I$ et $a \in I$,
$f$ est dérivable en $a$ si la limite du taux d’accroissement calculé en $a$ existe et est finie.
$f$ est dérivable sur $I$ si et seulement si $f$ est dérivable pour tout $x \in I$.
On définit alors la fonction dérivée $f’$ qui à tout $x$ associe le nombre dérivé de la fonction $f$ calculé au point $x$.
Exemple :
Considérons la fonction $f(x) = x^2$ définie sur $\mathbb{R}$.
Soit $a \in \mathbb{R}$,
Calculons le taux d’accroissement au point $a$:
$\dfrac{f(a+h) – f(a)}{h} = \dfrac{(a + h)^2 + a^2}{h} = \dfrac{a^2 + 2ah + h^2 – a^2}{h} = \dfrac{2ah +h^2}{h} = 2a + h$
Puis on calcule la limite du taux d’accroissement :
$\lim \limits_{h \to 0} \dfrac{f(a+h) – f(a)}{h} = \lim \limits_{h \to 0} 2a + h = 2a$.
Or $2a$ est finie, donc $f'(a) = 2a$.
En outre, ce calcul est vrai pour tout $a \in \mathbb{R}$, ainsi, pour tout $x \in \mathbb{R}$, $f'(x) = 2x$.
Il est important de retenir le tableau contenant les dérivées usuelles suivantes qui peuvent être démontrées pour la plupart en suivant la méthode de l’exemple précédent :
Il faudra prêter attention au fait que l’ensemble de dérivabilité de la fonction racine carrée n’est pas égal à son ensemble de définition : elle est définie sur $\mathbb{R}_+$ et est dérivable sur $\mathbb{R}_+^*$.
Opérations et dérivées
Opérations et dérivées
Soient $u$ et $v$ deux fonctions définies et dérivables sur $I$.
1) Dérivée d’une somme
La dérivée d’une somme de fonctions est égale à la somme des dérivées de chaque fonction : c’est à dire
$(u + v)’ = u’ + v’$.
Par exemple $f(x) = x^2 + \dfrac{1}{x}$.
Il faut dans un premier temps chercher le domaine de définition et l’ensemble de dérivabilité.
La fonction $u(x) = x^2$ est définie et dérivable sur $\mathbb{R}$ et la fonction $v(x) = \dfrac{1}{x}$ est définie et dérivable sur $\mathbb{R}^*$.
Ainsi, la fonction $f$ est définie et dérivable sur $\mathbb{R}^*$.
Pour $x \in \mathbb{R}^*, \ f'(x) = 2x + \dfrac{-1}{x^2}$.
2) Dérivée du produit d’une fonction par un réel $k$
La formule est la suivante : $(ku)’ = k \times u’$ avec $k \in \mathbb{R}$.
Exemple, on souhaite déterminer la dérivée de $f(x) = -2x^2$.
La fonction $f$ est définie et dérivable sur $\mathbb{R}$ ainsi:
pour tout réel $x$, $f'(x) = -2 \times (2x) = -4x$.
3) Dérivée de l’inverse d’une fonction
La formule est $\left ( \dfrac{1}{v} \right )’ = \dfrac{-v’}{v^2} $ pour tout $x \in I$ et il faudra veiller à ce que $v(x) \neq 0$.
Exemple, considérons la fonction $f(x) = \dfrac{1}{x+1}$.
$f$ est définie et dérivable sur $\mathbb{R} \backslash \{-1\}$:
Pour tout réel $x$ différent de $-1,\ f'(x) = \dfrac{-1}{(x+1)^2}$.
4) Dérivée du produit de deux fonctions
La dérivée d’un produit est donnée par la formule suivante :
$(uv)’ = uv’ + u’v$.
Exemple : Soit $f(x) = (3x + 1)\times \sqrt{x}$,
la fonction $x \mapsto 3x + 1$ est définie et dérivable sur $\mathbb{R}$
La fonction $x \mapsto \sqrt{x}$ est définie sur $\mathbb{R}_+$ et dérivable sur $\mathbb{R}_+^*$.
Ainsi, $f$ est définie sur $\mathbb{R}_+$ et dérivable sur $\mathbb{R}_+^*$.
Pour tout $x \in \mathbb{R}_+^*, \ f'(x) = 3 \times \sqrt{x} + (3x + 1) \times \dfrac{1}{2\sqrt{x}}$.
5) Dérivée du quotient de deux fonctions
La dérivée d’un quotient est $\left ( \dfrac{u}{v} \right )’ = \dfrac{u’v – uv’}{v^2}$. La fonction $v$ ne s’annulant pas.
Exemple : Soit $f(x) = \dfrac{2x + 1}{x – 4}$ définie et dérivable sur $\mathbb{R} \backslash \{4 \}$,
Pour tout $x$ différent de $4$,
$f'(x) = \dfrac{2(x – 4) – (2x + 1) \times 1}{(x – 4)^2}$.
$f'(x) = \dfrac{-9}{(x – 4)^2}$.
Variations de fonctions
Variations de fonctions
Propriété :
Soit $f$ une fonction dérivable sur $I$,
si pour tout $x \in I$, la dérivée est strictement positive alors la fonction $f$ est strictement croissante sur $I$.
si pour tout $x \in I$, la dérivée est strictement négative alors la fonction $f$ est strictement décroissante sur $I$.
Pour étudier les variations d’une fonction, on commence par calculer la dérivée de la fonction puis on étudie le signe de la dérivée.
On conclut enfin sur les variations de la fonction.
Exemple :
Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x) = x^2 + 3x + 1$ et dérivable sur $\mathbb{R}$.
On souhaite étudier les variations de la fonction $f$.
La dérivée de la fonction $f$ est $f'(x) = 2x + 3$.
On étudie le signe de la dérivée :
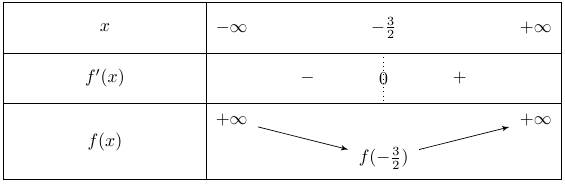
$f'(x) > 0 \iff 2x + 3 > 0 \iff x > \dfrac{-3}{2}$
De même, $ f'(x) < 0 \iff x < \dfrac{-3}{2}$.
On peut alors remplir le tableau de signe de la dérivée.
Pour $x \in ]- \infty; -\frac{3}{2}[$, la dérivée est strictement négative, la fonction $f$ est donc strictement décroissante sur cet intervalle.
Pour $x \in ]-\frac{3}{2}, + \infty; [$, la dérivée est strictement positive, la fonction $f$ est donc strictement croissante sur cet intervalle.
Une flèche vers le haut symbolise une fonction croissante alors qu’une flèche vers le bas marque une fonction décroissante.
On indique également aux extrémités des flèches la valeur de la fonction au point correspondant lorsque l’on peut la calculer.
On obtient alors le tableau de variations de la fonction $f$ suivant que l’on écrit sous le tableau de signe :
On remarque que la fonction $f$ admet un minimum atteint en $x = – \dfrac{3}{2}$ ce qui correspond à $x = \dfrac{-b}{2a}$ lorsque le polynôme du second degré s’écrit $ax^2 + bx + c$.
Le tableau de variation permet donc d’étudier les extrema d’une fonction.