Écritures fractionnaires
Quotients et écritures fractionnaires
Définition
Un quotient est le résultat d’une division.
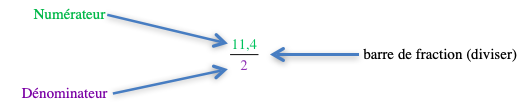
Exemple : 5,7 est le quotient de 11,4 par 2. On écrit
$11,4\div 2=5,7$
L’écriture fractionnaire de ce quotient est :$\dfrac{11,4}{2}$.
On le lit : « 11,4 sur 2 » ou « 11,4 demis »
$\dfrac{11,4}{2}$ est donc le « ? » dans l’égalité :
$2 \times ?=11,4$ (on cherche « combien de fois il y a 2 dans 11,4 »)
Fraction
Si le numérateur et le dénominateur sont des nombres entiers alors l’écriture fractionnaire est une fraction.
Exemple : $\dfrac{19}{2}$
Propriétés :
1) Une écriture fractionnaire traduit un partage équitable :
2) Un même nombre a plusieurs écritures fractionnaires.
On obtient une écriture fractionnaire égale à la première en multipliant ou en divisant le numérateur et le dénominateur par un même nombre non nul (différent de zéro).
Exemples :
$\dfrac{35}{25}=\dfrac{35\div 5}{25\div 5}=\dfrac{7}{5}$ et
$\dfrac{3}{20}=\dfrac{3\times 2}{20\times 2}=\dfrac{6}{40}$
Ici on a simplifié la fraction.
Commentaire
Les fractions sont très importantes pour la suite du collège. On les utilise aussi dans la vie de tous les jours :
une baguette et demi ($1+\dfrac{1}{2}$ )
les quatre cinquièmes ($\dfrac{4}{5}$ ) des élèves du collège mangent à la cantine…
Multiplication d'un nombre par une fraction
Multiplication d’un nombre par une fraction
Définition
Calculer une fraction d’un nombre c’est multiplier ce nombre par cette fraction.
Exemple :
Calculer les $\dfrac{3}{5}$ de $20$ revient à calculer $\dfrac{3}{5}\times 20$ .
Trois méthodes de calculs
1) $\dfrac{3}{5}\times 20=\dfrac{3\times 20}{5}=\dfrac{60}{5}=12$ (méthode qui fonctionne dans tous les cas)
On multiplie d’abord le nombre par le numérateur puis on divise le résultat par le dénominateur
2) $\dfrac{3}{5}\times 20=\dfrac{20}{5}\times 3=4\times 3=12$ (méthode qui ne fonctionne que si cette division est exacte)
On divise d’abord le nombre par le dénominateur puis on multiplie le résultat par le numérateur
3) $\dfrac{3}{5}\times 20=0,6\times 20=12$ (méthode qui ne fonctionne que si cette division est exacte)
On calcule l’écriture décimale de la fraction puis on multiplie ce quotient par le nombre.
Autre exemple
Calculons $\dfrac{5}{3}$ de 20, soit :
Attention : $5\div3$ et $20\div3$ n’ont pas de quotient décimal exact (ces divisions « ne s’arrêtent pas ») donc seule la première méthode peut être utilisée.
$\dfrac{5}{3}\times 20=\dfrac{5\times 20}{3}=\dfrac{100}{3}$
On ne peut pas écrire la valeur exacte de ce nombre sous forme décimale.
A chacun de choisir la méthode qui convient le mieux suivant chaque cas !
Commentaire :
Ces calculs ne sont pas difficiles, il faut juste bien connaitre les tables de multiplications.
Fractions décimales
Fractions décimales
Définition
Une fraction décimale est une fraction dont le dénominateur est 1 ; 10 ; 100 ; 1000…
Exemples :
$\dfrac{45}{100}$ ; $\dfrac{4}{1000}$ ; $\dfrac{25}{1}$ et $\dfrac{7}{10}$ sont des fractions décimales.
$\dfrac{4}{7}$ n’est pas une fraction décimale.
Propriété
Tout nombre décimal peut s’écrire sous la forme :
- d’une fraction décimale,
- de la somme de fractions décimales,
- de la somme d’un nombre entier et d’une ou plusieurs fractions décimales (ce sont des « décompositions décimales »).
Exemples :
$\dfrac{6}{10}=0,6$
On lit « 6 dixièmes » et 6 est bien le chiffre des dixièmes dans $0,6$.
( $0,6$ a un chiffre après la virgule et $10$ a un zéro).
$\dfrac{3507}{1000}=3,507$
On lit « 3 507 millièmes » et 7 est bien le chiffre des millièmes dans $3,507$.
($3,507$ a trois chiffres après la virgule et $1000$ a trois zéros)
On peut aussi écrire :
$\dfrac{3507}{1000}=\dfrac{3}{1}+\dfrac{5}{10}+\dfrac{0}{100}+\dfrac{7}{1000}$
Ou encore :
$\dfrac{3507}{1000}=\dfrac{3}{1}+\dfrac{507}{1000}$
Attention : un même nombre décimal est égal à plusieurs fractions décimales.
$3,507=\dfrac{3507}{1000}=\dfrac{35070}{10000}=\dfrac{350700}{100000}$
(En effet 3,507=3,5070=3,50700)
Commentaire : Pour bien comprendre cette fiche il faut déjà être à l’aise avec la notion de nombre décimal ainsi qu’avec le nom et le rôle de chaque chiffre (dixième, centième…)



